Having recently addressed a 1-D problem, today I aim to solve a 2-D problem.
The goal of this post is to study the necessary formulas before solving an example.
First, the basic element is a triangle with three nodes, and the temperature function is given as follows.
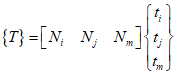
Where, ${t_i}$, ${t_j}$ and ${t_m}$ are the nodal temperatures, and the shape functions are as follows.
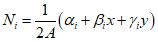
The same applies to ${N_j}$, ${N_m}$, and here, $\alpha $, $\beta $, and $\gamma $ are as explained in the previous post(26_Constant-Strain Triangular element), so I won't go into detail.
Unlike CST elements, in the three-node triangular element for heat transfer, only the temperature at each node is treated as basic unknown.
In thermal stress problems, a gradient matrix similar to the strain matrix used can be defined as follows.
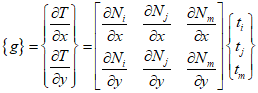
Using the strain matrix to express the above equation in matrix form, it becomes as follows, and by arranging the above equations, the $B$ matrix can be obtained.
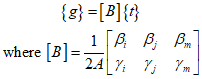
The relationship between heat flux/temperature gradient and the material property matrix $D$ can be represented as follows.
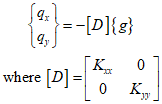
The element stiffness can be represented as follows.
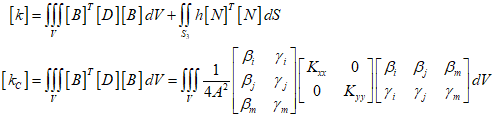
Where, ${k_C}$ is the heat transfer part of the $k$ matrix.
Considering a constant thickness within the element and the constant terms, it can be summarized as follows.
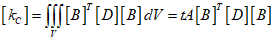
The convection part of the stiffness matrix can be defined as follows.
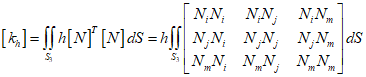
If the surface between nodes $i$ and $j$ is exposed to convection, then ${N_m}$ becomes zero along the $i-j$ surface.
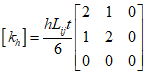
The force matrix can be represented as follows.
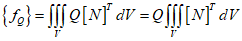
Where, if the heat source($Q$) is constant, it is as follows.
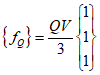
Therefore, the force matrix addressed in the previous post(44_1-D Heat Transfer Finite Element Formulation(2)) can be represented as follows.
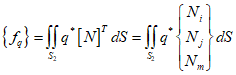
'Finite Element Method' 카테고리의 다른 글
| 49_Heat Transfer with Mass Transport (0) | 2024.01.18 |
|---|---|
| 48_2-D Heat Transfer Example (0) | 2024.01.17 |
| 46_1-D Heat Transfer Example(2) (0) | 2024.01.15 |
| 45_1-D Heat Transfer Example (0) | 2024.01.14 |
| 44_1-D Heat Transfer Finite Element Formulation(2) (1) | 2024.01.13 |