Similar to the problem addressed in the previous post, in this post, I'll solve an example that calculates the temperature distribution and rate of heat in a rod fixed to a wall, without any insulated parts.

In the figure above, the temperature at the left end is fixed at ${100^{\text{o}}}{\text{C}}$, ${K_{xx}} = 60{\text{W/(m}}{{\text{ - }}^{\text{o}}}{\text{C)}}$, radius is $50mm$, $h = 800{\text{W/(m}}{{\text{ - }}^{\text{o}}}{\text{C)}}$, and ${T_\infty } = {10^{\text{o}}}{\text{C}}$.
In this example, the rod will be divided into three elements each of $75mm$ in length for calculation. The left end of the rod has no convective heat loss, but convective heat loss occurs in all other parts. Calculating the stiffness matrix for each element, it is as follows.
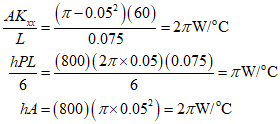

In the first element, the temperature is fixed at the left end, and the right end is inside the rod, not exposed to fluid movement, so there is no convection. Therefore, the convection term of the stiffness matrix is zero, and it can be represented by the above equation. On the other hand, the third element must consider the convection term due to heat loss at the right end, and it can be represented as follows.
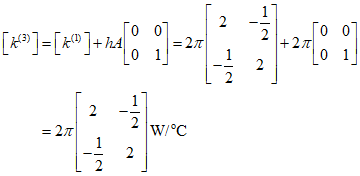
In the element force matrix, $Q=0$, ${q^*}=0$, and only the $h{T_\infty }$ term exists. Therefore, it can be represented as follows.
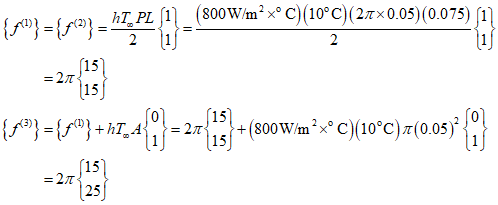
By assembling the element stiffness matrix and the element force matrix, the following system of equations can be obtained.

Therefore, solution can be calculated as follows.
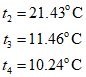
The heat flux for the first element can be calculated as follows.
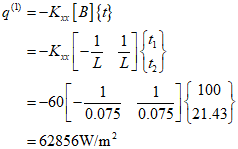
Finally, the rate of heat flow $\bar q$ can be calculated by multiplying it by the cross-sectional area.
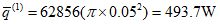
'Finite Element Method' 카테고리의 다른 글
| 48_2-D Heat Transfer Example (0) | 2024.01.17 |
|---|---|
| 47_2-D Heat Transfer Finite Element Formulation (0) | 2024.01.16 |
| 45_1-D Heat Transfer Example (0) | 2024.01.14 |
| 44_1-D Heat Transfer Finite Element Formulation(2) (1) | 2024.01.13 |
| 43_1-D Heat Transfer Finite Element Formulation (0) | 2024.01.12 |