Today, I plan to solve a problem related to finite elements, something I haven't done in a while. The problem is as follows.
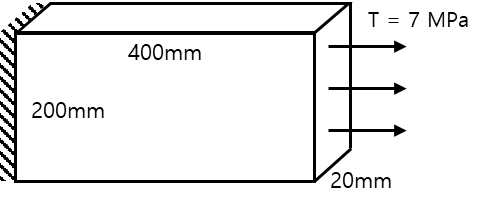
Here, the goal is to fine the nodal displacements and element stresses. $E$ is $210GPa$, and Poission's ratio is 0.3.
First, discretize the plate into two elements and simplify the tensil surface traction into nodal forces for calculation.


Applying $\left[ F \right] = \left[ K \right]\left\{ d \right\}$, the general governing equation used in structural analysis problems, it can be represented as follows.

To create the global stiffness matrix, the element stiffness matrices must be assembled. The element stiffness matrix is as follows.

Starting with the node at the bottom left of the first element and moving counterclockwise, denoting the nodes as $i, j, m$, the $B$ matrix can be calculated as follows.
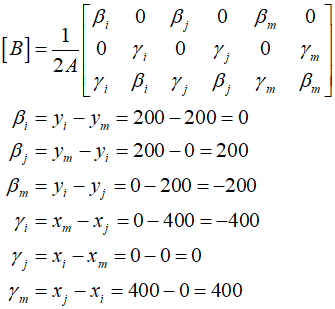
Subsitute a values
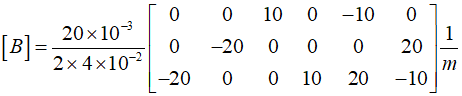
In the plane stress, the $[D]$ matrix can be calculated as follows.
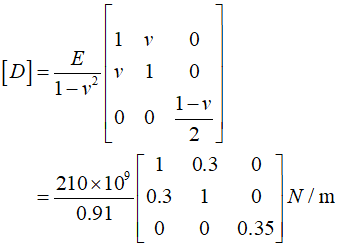
Therefore


Since the degrees of freedom for the stiffness matrix of element 2 do not apply to all nodes, it is necessary to expand for the entire nodes and calculate the global stiffness matrix.

$\left[ K \right]$ into $\left[ F \right] = \left[ K \right]\left\{ d \right\}$.
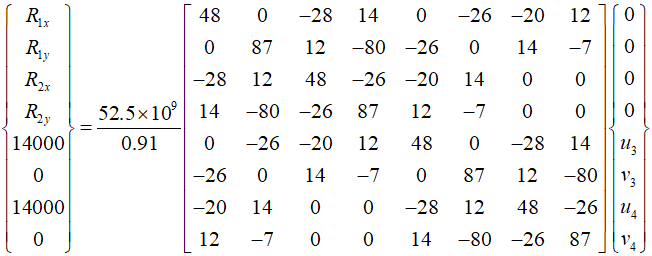
Applying the boundary conditions, it can be summarized as follows.
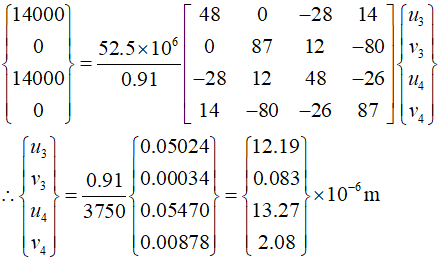
Now, calculate the stresses in each element.

For element 2 is as follows.
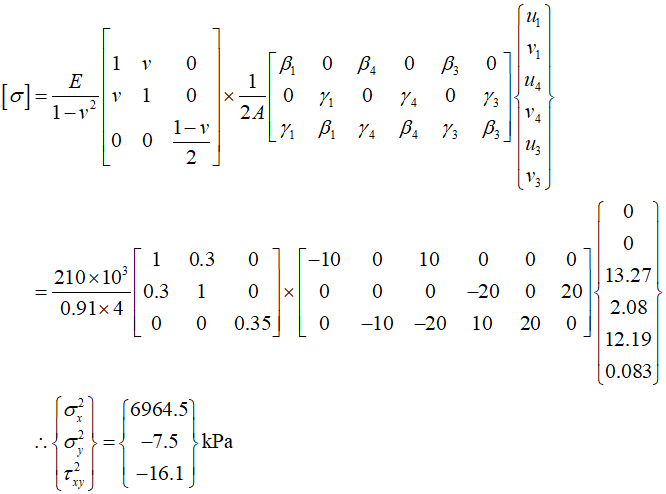
Therefore, the principle stresses can be calculated as follows.
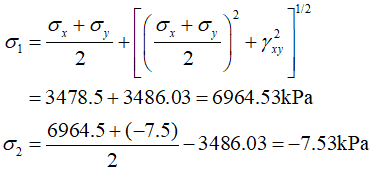
'Finite Element Method' 카테고리의 다른 글
| 94_Two-Point Gaussian Integration (0) | 2024.03.03 |
|---|---|
| 93_Linear Plane Quadrilateral Example (0) | 2024.03.02 |
| 49_Heat Transfer with Mass Transport (0) | 2024.01.18 |
| 48_2-D Heat Transfer Example (0) | 2024.01.17 |
| 47_2-D Heat Transfer Finite Element Formulation (0) | 2024.01.16 |