In the field of structural analysis and Finite Element Analysis (FEA), I intend to explain the process of deriving the stiffness matrix for a basic three-node bar element. Unlike previous postings(39_High Order Example), this time I plan to calculate the stiffness matrix of a three-node bar element using two-point Gaussian integration. A bar element with three nodes and two Gaussian points is as follows.
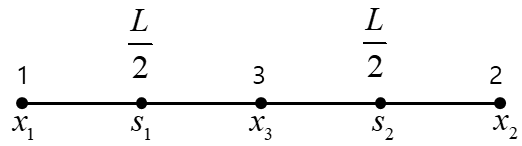
The previously derived stiffness matrix is as follows.
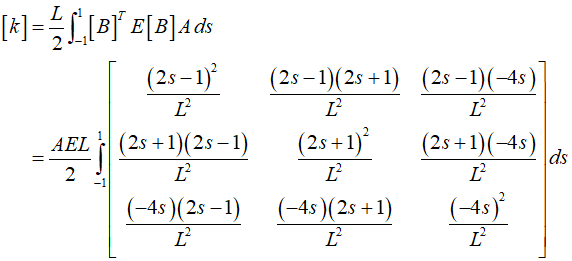
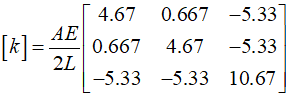
To approximate each element of the stiffness matrix using two-point Gaussian integration, it is necessary to use two Gaussian points (${s_1} = - 0.57735,\,{s_2} = 0.57735$), and a weight (${W_1} = {W_2} = 1$).
Each element of the stiffness matrix is calculated by multiplying the evaluation values at the Gaussian points by the weight, and then summing them all. Therefore, the stiffness matrix is calculated for each element as follows.
1-1 element
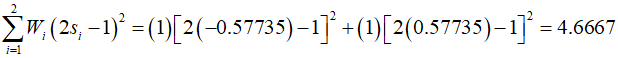
2-1 element
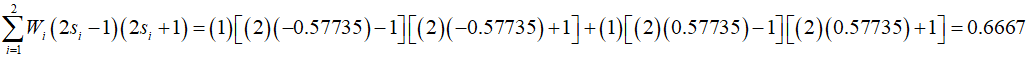
1-3 element

2-2 element

2-3 element

3-3 element
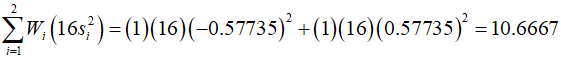
Through the element-wise stiffness matrix, the overall stiffness matrix can be obtained.
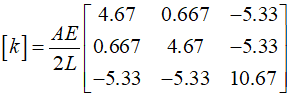
It can be varified that the stiffness matrix obtained using Gaussian integration is identical to the results obtained through direct explicit integration.
The use of Gaussian integration is a very efficient method for approximating integrals in FEA. As seen in the results above, instead of directly calculating complex integrals, approximation values can be used to effectively calculate the elements of the stiffness matrix. Additionally, because it offers both accuracy and computational efficiency, it is an important method widely used in FEA.
'Finite Element Method' 카테고리의 다른 글
| 96_Heat Flux Example (0) | 2024.03.05 |
|---|---|
| 95_Tetrahedral Element Example (0) | 2024.03.04 |
| 93_Linear Plane Quadrilateral Example (0) | 2024.03.02 |
| 91_Plane Stress Example (0) | 2024.02.29 |
| 49_Heat Transfer with Mass Transport (0) | 2024.01.18 |