Gaussian quadrature, unlike Newton-Cotes quadrature, optimizes the position of sampling points instead of creating them at uniform intervals, allowing for more accurate integration.
Therefore, Gaussian quadrature can perform more accurate integration with fewer sampling points.
The generalization of the midpoint rule can be represented as follows.

Where ${W_i}$ are the weights, and they are determined as follows based on the number of points.

To approximate the definite integral, the function is evaluated at multiple sampling points($n$), and each value is multiplied by its corresponding weight ${W_i}$, then summed.
The Gauss method selects sampling points to achieve the most effective accuracy for a given number of points. Typically, these points are symmetrically arranged about the center, and symmetrically paired points share the same weight.
Generally, an integration using $n$ Gauss points is exact for polynomials of degree $2n-1$ or less.
2-point formula
Explaining by example, consider the two-point Gauss formula.
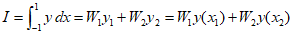
Given the existence of four unknowns, a cubic function is assumed as follows.
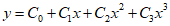
Generally, with four parameters in a 2-point formula, the Gauss formula can accurately predict the area under the curve.

However, since Gauss points are symmetrically located, ${W_1} = {W_2}$ and ${x_1} = {x_2}$. Therefore,

If the error $e = A - {A_G}$ is desired to vanish for any ${C_0}$ and ${C_2}$, it follows that
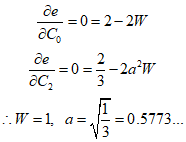
'Finite Element Method' 카테고리의 다른 글
| 37_Element Stress (1) | 2024.01.06 |
|---|---|
| 36_Gaussian Quadrature Example (0) | 2024.01.05 |
| 34_Newton-Contes Quadrature (1) | 2024.01.03 |
| 33_Isoparametric Formulation of the Bar element (0) | 2024.01.02 |
| 32_LST example (0) | 2024.01.01 |