In this post, I'll solve an example of the LST element which was explained in previous post.

The triangle has a six nodes, with a height of $h$ and a width of $b$
Displacement can be calculated as follows using the coordinates of the six nodes.
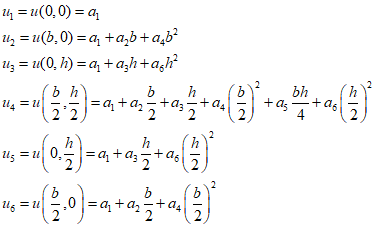
Upon rearranging for ${a_i}$

By substituting the two equations into the displacement function, it can be expressed as follows.
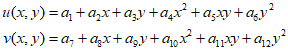

This can be represented in the form of a shape function as follows.
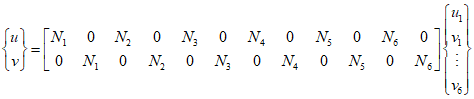
Additionally, each shape function is as follows.
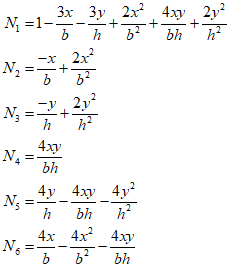
Performing the necessary differentiation to calculate the element displacement results in $\beta $ and $\gamma $ being as follows.

Therefore, It can be represented as follows.
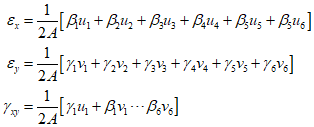
Therefore,the stiffness matrix for an element with a constant thickness can be obtained.
'Finite Element Method' 카테고리의 다른 글
| 34_Newton-Contes Quadrature (1) | 2024.01.03 |
|---|---|
| 33_Isoparametric Formulation of the Bar element (0) | 2024.01.02 |
| 31_Linear-Strain Triangle element (1) | 2023.12.31 |
| 30_Rectangular Element (0) | 2023.12.30 |
| 29_CST example (0) | 2023.12.29 |