I'll study one of the numerical integration methods, the Newton-Cotes integration. The Newton-Cotes method approximates the integrand with a polynomial for integration, with the trapezoidal rule and Simpson's rule being typical examples.
The Newton-Cotes method is not generally used as it does not yield results as accurate as the Gauss integration method.
When there is the following definite integral,

When the sampling points of $y(x)$ are placed at equal intervals, it can be represented as follows.

Where the ${C_i}$ represents the Newton-Cotes constant for the ith interval, and $h$ is the integration interval. The Newton-Cotes constants are predetermined for $i$ ranging from 1 to 6, where $i=1$ corresponds to the trapezoidal rule, and $i=2$ corresponds to Simpson's 1/3 rule.
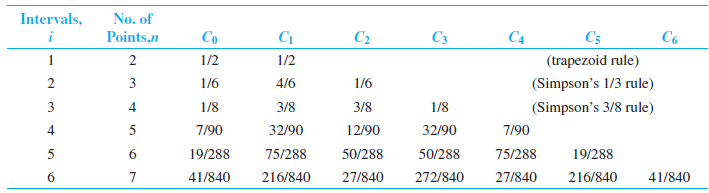
Moreover, the formulas for $i=3$ and $i=5$ have the same accuracy as those for $i=2$ and $i=4$, respectively. Therefore, it is preferable to use the formulas for $i=2$ and $i=4$.
'Finite Element Method' 카테고리의 다른 글
| 36_Gaussian Quadrature Example (0) | 2024.01.05 |
|---|---|
| 35_Gaussian Quadrature (2) | 2024.01.04 |
| 33_Isoparametric Formulation of the Bar element (0) | 2024.01.02 |
| 32_LST example (0) | 2024.01.01 |
| 31_Linear-Strain Triangle element (1) | 2023.12.31 |