This post will solve an example of obtaining the stiffness matrix using the Gaussian method, as covered in the previous post.
The stiffness matrix of the quadrilateral element is determined using the 4-point Gaussian quadrature rule.
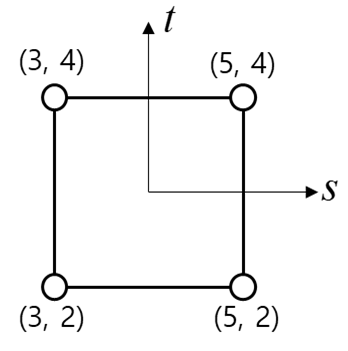
where $E=200 Gpa$ and $v=0.25$
Firstly, for a two-dimensional element, the stiffness matrix can be represented as follow.
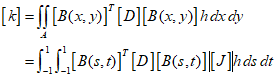
where $j$ is the $Jacobian$ matrix.
Using the 4-point rule to calculate the stiffness matrix of a Q4 element is referred to as 'full integration', representing the number of Gauss points necessary to accurately compute the stiffness matrix for elements with a regular shape.
This allows for precise calculation of the stiffness matrix.
Therefore, representing the stiffness matrix in the form of Gaussian integration, it can be expressed as follows.
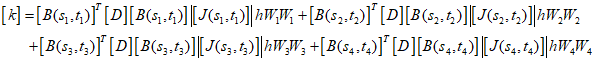
where ${s_1}={t_1}=-0.5773$, ${s_2}=-0.5773$, ${t_2}=0.5773$, ${t_t}=-0.5773$, ${s_4}={t_4}=0.5773$, and ${W_1}= {W_2}= {W_3}= {W_4}=1$.
Therefore, using the 4-point rule, it can be expressed as follows.
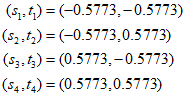
Therefore, substituting into the above stiffness matrix equation, it results as follows.
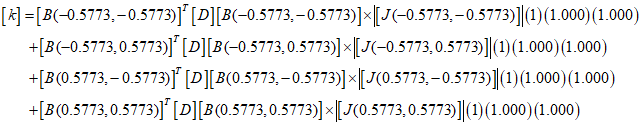
To derive $k$, $J$ is calculated at each Gauss point using the following equation.

Therefore,
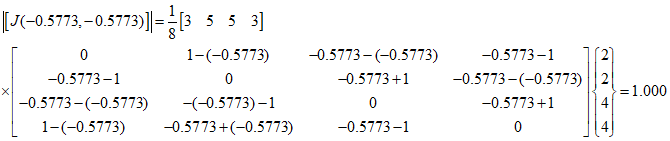
Thus, by calculating the remaining $J$.

The $B$ matrix can be calculated as follows.

Applying the above equation to the example, it can be calculated as follows.
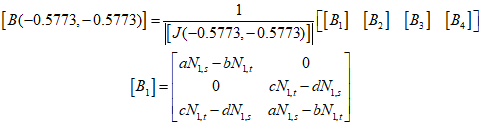
$a, b, c$ and $d$ can be calculated using the following equations.
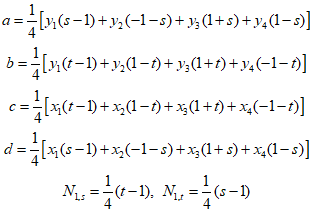
Therefore,
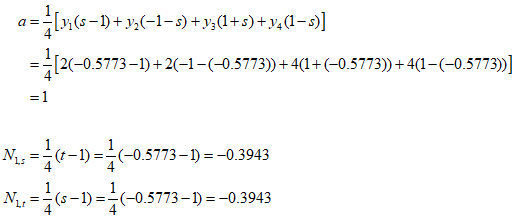
By arranging the above equations and calculating part of the $B$ and $D$ matrix.

Therefore, the stiffness matrix can be derived as follows.
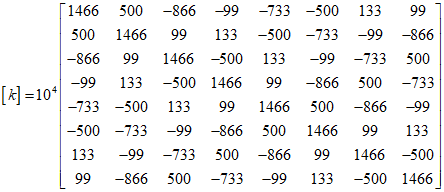
'Finite Element Method' 카테고리의 다른 글
| 38_High Order Shape Function (0) | 2024.01.07 |
|---|---|
| 37_Element Stress (1) | 2024.01.06 |
| 35_Gaussian Quadrature (2) | 2024.01.04 |
| 34_Newton-Contes Quadrature (1) | 2024.01.03 |
| 33_Isoparametric Formulation of the Bar element (0) | 2024.01.02 |