In this post, I'll study the isoparametric formulation of the plane 4-node quadrilateral (Q4) element stiffness matrix.
Additionally, Gauss integration will be used to calculate the stress at given points in a plane quadrilateral element.
The isoparametric element equations are formulated using the natural coordinate system $s$, defined by the element geometry. The axial coordinate $s$ is affixed to the bar and extends along its length.
The relationship between the natural coordinate system $s$ and the global coordinate system $x$ is used in the formulation of the element equations.
Taking a 1D bar element with two degrees of freedom as an example, each node has axial displacements ${u_1}$ and ${u_2}$ related to the global x-axis in the axial direction.
When the $s$ and x-axes are parallel, it can be expressed as follows.
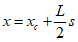
${x_c}$ is the central coordinate, and it can be expressed using ${x_1}$ and ${x_2}$ as follows.

To relate s and $x$, the following equation is used, where $s$ is greater than -1 and less than 1.
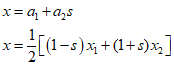
In the matrix form.
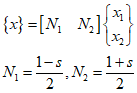
Through the above equation, any $s$-coordinate within the element can be mapped to an $x$-coordinate.
Additionally, the shape functions must be continuous within the domain and differentiability must be ensured.
If the displacement function is defined by the shape functions, it is as follows.

To define the stiffness matrix, the $B$ matrix is defined. Strain can be defined as the derivative of displacement
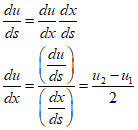
Using the equation in terms of $x$, it can be summarized as follows.
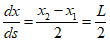
Therefore, the $B$ matrix can be defined as follows.
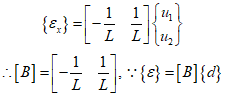
The stiffness matrix can be defined as follows.
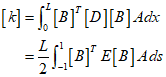
In a 1D element, it can be represented as follows.
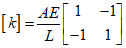
'Finite Element Method' 카테고리의 다른 글
| 35_Gaussian Quadrature (2) | 2024.01.04 |
|---|---|
| 34_Newton-Contes Quadrature (1) | 2024.01.03 |
| 32_LST example (0) | 2024.01.01 |
| 31_Linear-Strain Triangle element (1) | 2023.12.31 |
| 30_Rectangular Element (0) | 2023.12.30 |