In this post, I'll explain the stiffness matrix and equations of the Linear-Strain Triangle(LST) element, which differs from the Constant-Strain Triangle(CST) element covered in the last post.
Unlike CST, LST has six nodes and twelve degrees of freedom, and its displacement function is a quadratic function, unlike the linear function in CST.
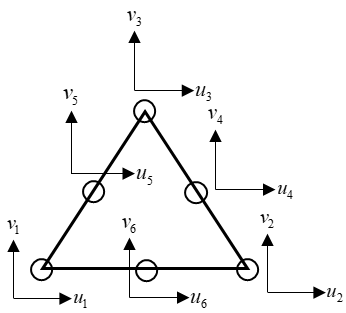
In LST, the node displacements are as follows.
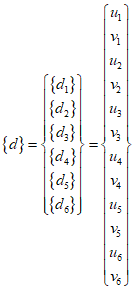
And the quadratic displacement function can be represented as follows.

All items of the Pascal's triangle are used as shape functions.
As previously explained, linear functions are used in CST elements, while quadratic functions are employed in LST elements being discussed in this post. The displacement function, when expressed in matrix form, is as follows.
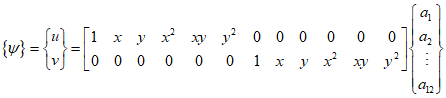
By substituting coordinates into u and v as shown below, the coefficients of a can be obtained

Therefore, it can be summarized as follows.

The displacement equation can be obtained as follows.

The stress is as follows.

Therefore, the stiffness matrix and $B$ matrix can be defined as follows.

Therefore, the element equation is as follows.

'Finite Element Method' 카테고리의 다른 글
| 33_Isoparametric Formulation of the Bar element (0) | 2024.01.02 |
|---|---|
| 32_LST example (0) | 2024.01.01 |
| 30_Rectangular Element (0) | 2023.12.30 |
| 29_CST example (0) | 2023.12.29 |
| 28_Stress Strain relationship (0) | 2023.12.28 |