Continuing from the previous post, I intend to write about the strain in Constant-Strain Triangular(CST) elements.
The strain of a two-demensional element is as follows.
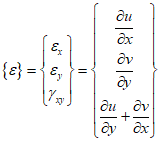
In the CST element, the strain within the element is always constant, and the edges remain straight even when the element deforms. Using the $u(x,y)$, $v(x,y)$ equations frome the previous post, it can be transformed as follows.

Additionally, the derivatives of the shape functions can be defined using the following equation.
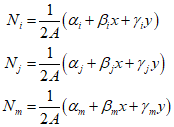

Using this, when transformed with respect to the derivative of $u$, it becomse,

Therefore, modifying the initial strain equation for a two-dimensional element results in

'Finite Element Method' 카테고리의 다른 글
| 29_CST example (0) | 2023.12.29 |
|---|---|
| 28_Stress Strain relationship (0) | 2023.12.28 |
| 26_Constant-Strain Triangular element (0) | 2023.12.26 |
| 25_Castigliano's First Theorem (0) | 2023.12.25 |
| 24_Castigliano's Second Theorem (0) | 2023.12.24 |