Continuing from the last post, today I intend to explain Castigliano's First Theorem.
Castigliano's First Theorem can be summarized as 'the partial derivative of the strain energy of any elastic structure with respect to displacement is equal to the load' and I intend to explain this using the corresponding equation.
In an elastic structure where $n$ external forces ${P_1},{P_2}, \cdots ,{P_n}$ are applied, and corresponding displacements ${u_1},{u_2}, \cdots ,{u_n}$ exist, the equilibrium equation of strain energy using displacement is as follows.
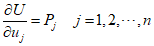
The strain energy of an elastic body is
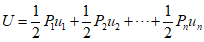
When a stiffness $k$ exists according to the force-displacement relationship, the equation $P = ku$ holds true.

Which represents the force at point $i$ due to the displacement applied at point $j$, and the strain energy can be expressed as follows.
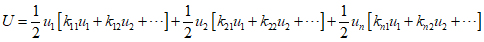
Maxwell-Betti's reciprocal theorem ${k_{ij}} = {k_{ji}}$.

Therefore, differentiating the strain energy with respect to displacement ${u_1}$ yields the applied force ${P_1}$ at that point, and it can be summarized as follows.
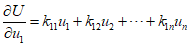
Therefore

When dealing with an elastic structure, formulated an demonstrated Castigliano's First Theorem mathematically.
'Finite Element Method' 카테고리의 다른 글
| 27_Element Strain (0) | 2023.12.27 |
|---|---|
| 26_Constant-Strain Triangular element (0) | 2023.12.26 |
| 24_Castigliano's Second Theorem (0) | 2023.12.24 |
| 23_2D Stress and Strain (1) | 2023.12.23 |
| 19_Weighted residual methods (0) | 2023.12.19 |