Continuing from the previous post, I intend to write about stress-strain relationship
In the plane, the stress-strain relationship can be expressed as follows.
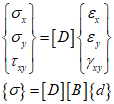
Using the principle of minimum potential energy to express the equation of the CST element in its weak form yields the following.

And the strain energy is

Therefore The potential energy of the body forces is as follows.

Where $\psi $ is the general displacement function, and $X$ is the weight density matrix.
The potential energy of a concentrated load is as follows.

Where $d$ is nodal displacements, and $P$ is the concentrated external loads.
The potential energy of a distributed loads load is as follows.

Where ${T_S}$ is the surface tractions(distributed loads), ${\psi _S}$ is the field of surface displacements through the surface trations act, $S$ is the surfaces over which the tractions ${T_S}$ act.
Therefore, summarizing the equation, it is as follows.
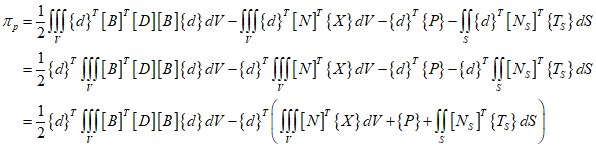
The total load system $f$ on an element is

Each term represents body forces, concentrated forces, and surface tractions, respectively. Therefore, the equation can be summarized as follows.

Taking the partial derivative with respect to displacement,

Therefore
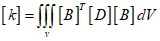
'Finite Element Method' 카테고리의 다른 글
| 30_Rectangular Element (0) | 2023.12.30 |
|---|---|
| 29_CST example (0) | 2023.12.29 |
| 27_Element Strain (0) | 2023.12.27 |
| 26_Constant-Strain Triangular element (0) | 2023.12.26 |
| 25_Castigliano's First Theorem (0) | 2023.12.25 |