Today, I intend to explain the last of the finite element equation methods : the weighted residual methods
Among them, the most widely used Galerkin's method will be explained.
Assuming there is a differential equation $Du(x)=f(x)$ for $u(x)$, and the approximate solution for $u$ is denoted as $\hat u$, then since $u \ne \hat u$, $Du(x)=f(x)$ is satisfied, but $D\hat u - f \ne 0$.
This is referred to as the 'residual', and let's define it as $R \equiv D\hat u - f$.
Therefore defining this approximate solution as a linear combination of some basis functions turns it into an optimization problem that minimizes the residual.
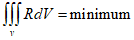
In the residual method, the weighting of the residual is adjusted to minimize its value over the entire domain. Representing the weight function as $W$, the general form is as follows.
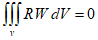
In the Galerkin method, the basis used for the approximation function is also used as the weight function. The residual method varies depending on which weight function is used. When applying the Galerkin method, it can be expressed as follows.

Using this, let's define the stiffness equation fora bar element. Consider a bar element as follows.

differential governing equations as

where $u$ is the axial displacement function along the element in the x direction and $A$ and $E$ are written as though they were function of $x$ in the general form of the differential equation
Upon rearranging the equation, it becomes
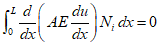
integration

Due to the need to satisfy boundary conditions, the following equation is used. ( ${N_1} = 1 - \frac{x}{L},\,{N_2} = \frac{x}{L}$ )
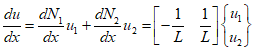
Therefore, it can be summarized as follows.
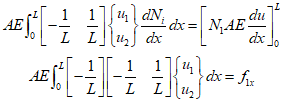
where ${f_{1x}} = AE\frac{{du}}{{dx}}$.
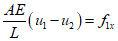
${N_1}$ is also the same.

Therefore, the equation $KU = F$ can be derived.
'Finite Element Method' 카테고리의 다른 글
| 24_Castigliano's Second Theorem (0) | 2023.12.24 |
|---|---|
| 23_2D Stress and Strain (1) | 2023.12.23 |
| 18_Principle of virtual work (0) | 2023.12.18 |
| 17_Direct Methods examples (0) | 2023.12.17 |
| 16_Direct Methods (0) | 2023.12.16 |