The Runge-Kutta method achieves the accuracy of the Taylor series method without the need to calculate higher-order derivatives. Although various variations exist, it can be generally expressed in the following forms.
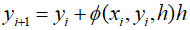
Here, $\phi ({x_i},{y_i},h)$ is referred to as the increment function, and it can typically be written as follows.
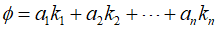
The second-order version of the above formula can be expressed as follows.

To use the above formula, it is necessary to determine the values of the constants ${a_1}$, ${a_2}$, ${p_1}$, and ${q_11}$. For this, the second-order Taylor series of ${y_{i + 1}}$ must be expressed as a function of ${y_i}$ and $f({x_i},{y_i})$.
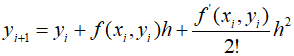
Here, $f'({x_i},{y_i})$ is determined by chain-rule differentiation.
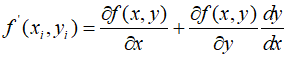
The above equations can be summarized as follows.

The basic strategy of the Runge-Kutta method is to make the above equations equicalent and to determine the values of ${a_1}$, ${a_2}$, ${p_1}$, and ${q_11}$ using algebraic methods. To do this, an expansion of the Taylor series for a two-variable functions is first required.
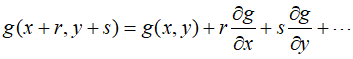
Therefore,
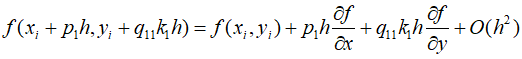
By substituting the above results into the equations, they can be arranged as follows.
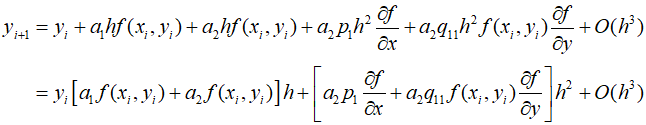
For the two equations to be equivalent, the following conditions must be satisfied.
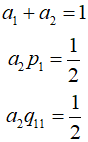
There are three simultaneous equations and four unknown constants. Since there is one more unknown than there are equations, there is no unique set of constants that satisfies the equations. Therefore, by assuming a value for one of the constants, the values of the remaining three can be determined.
'Numerical Methods' 카테고리의 다른 글
| 161_Richardson's Extrapolation (0) | 2024.05.09 |
|---|---|
| 160_Simpson's 3/8 Rule (0) | 2024.05.08 |
| 159_Multiple SImpson's 1/3 Rule (0) | 2024.05.07 |
| 158_Simpson's Rules (0) | 2024.05.06 |
| 157_Multiple Trapezoidal Rule (0) | 2024.05.05 |