Continuing from the previous posting, another method to estimate a more accurate integral value is by connecting points using higher-degree polynomials. The formula for integrating under such polynomials is known as Simpson's rule.
Simpson's $1/3$ rule can be expressed using a second-degree interpolating polynomial as follows.

If $a$ and $b$ are designated as ${x_0}$ and ${x_2}$, respectively, and ${f_2}(x)$ is represented as a second-order Lagrnage polynomial, the integral can be expressed as follows.
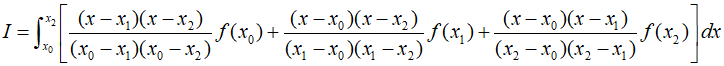
To summarize succinctly, it can be expressed as follows.

Here, $h = (b - a)/2$. This formula is known as Simpson's $1/3$ rule and is the second Newton-Cotes colsed integration formula. The term $"1/3"$ is derived from $h$ being divided by $3$ in the formula. Similarly, it can also be expressed in other forms.
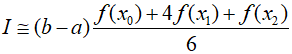
In this posting, I intend to explain the derivation of the above formula. Simpson's $1/3$ rule can be derived by integrating the forward Newton-Gregory interpolation polynomial.
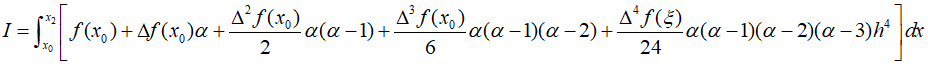
Here, the polynomial includes terms up to the fourth degree, not just the third degree, and the integration limits are from ${x_0}$ to ${x_2}$. Therefore, when simplifying and substituting in the integral, the limits are from $\alpha = 0$ to $2$.
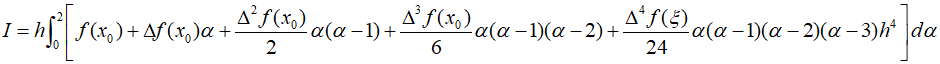
When intergrated, it can be expressed as follows.
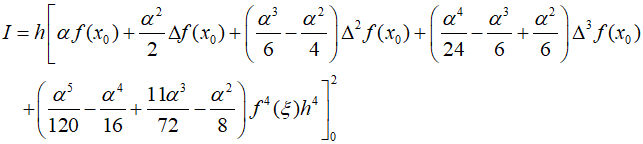
Therefore,
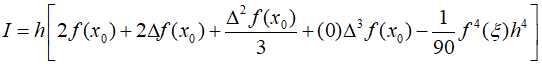
Here, the coefficient of the third divided difference is zero because $\Delta f({x_0}) = f({x_1}) - f({x_0})$ and ${\Delta ^2}f({x_0}) = f({x_2}) - 2f({x_1}) + f({x_0})$. Therefore, it can be rewritten as follows.
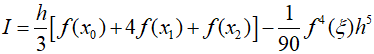
Therefore, the first term represents Simpson's $1/3$ rule, and the second term represents the truncation error.
'Numerical Methods' 카테고리의 다른 글
| 160_Simpson's 3/8 Rule (0) | 2024.05.08 |
|---|---|
| 159_Multiple SImpson's 1/3 Rule (0) | 2024.05.07 |
| 157_Multiple Trapezoidal Rule (0) | 2024.05.05 |
| 156_Trapezoidal Rule (0) | 2024.05.04 |
| 155_Least Squares Fit (0) | 2024.05.03 |