As explained in the previous posting, Simpson's $1/3$ rule can only be used when the intervals are equidistant and there are an even number of segments with an odd number of points. To address scenarios that don't meet these requirement, this posting will introduce Simpson's $3/8$ rule, which can be used alongside the $1/3$ rule to calculate cases with odd segments and an even number of points.
Similar to the derivation of the trapezoidal formula and Simpson's $1/3$ rule, the Simpson's $3/8$ rule involves fitting a third-order Lagrange polynomial to four point and intergrating it.
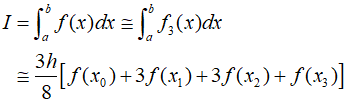
Here $h$ is equal to $(b-a)/3$, and since $h$ is multiplied by $3/8$, this equation is referred to as Simpson's $3/8$ rule. This is also the third Newton-Cotes closed integration formula. It can be expressed as follows.
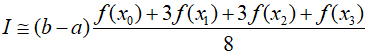
Therefore, the two internal points are assigned a weight of $3/8$, and the endpoints are given a weight of $1/8$. Consequently, the error in Simpson's $3/8$ rule can be expressed as follows.
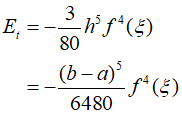
Due to the larger denominator in the equation, Simpson's $3/8$ rule can be slightly more accurate than the $1/3$ rule used previously. Although the $1/3$ rule is generally preferred for its simplicity and efficiency, the $3/8$ rule achieves third-order accuracy with three points and can be used when the number of segments is odd. In this example, I'll apply Simpson's $1/3$ rule to the first two segments and Simpson's $3/8$ rule to the remaining three segments to obtain a third-order accurate estimate for the entire interval.

For the interval from $a=0$ to $b=0.8$, initially use only Simpson's $3/8$ rule, dividing it into four equal segments for calculation.

Therefore,

Divide the interval into five segments and use both Simpson's $1/3$ and $3/8$ rule.

Apply Simpson's $1/3$ rule to the first two segments.

Apply Simpson's $3/8$ rule to the last three segments.

Therefore, the total integral can be obtained by adding the results of the two estimated values.

Therefore, it can be observed that applying both of Simpson's rules results in the least error.
'Numerical Methods' 카테고리의 다른 글
| 162_Runge-Kutta Methods (0) | 2024.05.11 |
|---|---|
| 161_Richardson's Extrapolation (0) | 2024.05.09 |
| 159_Multiple SImpson's 1/3 Rule (0) | 2024.05.07 |
| 158_Simpson's Rules (0) | 2024.05.06 |
| 157_Multiple Trapezoidal Rule (0) | 2024.05.05 |