To improve the calculation of simulaneous linear equations, iterative refinement methods have been used. Error correction techniques are used to enhance numerical integration results based on the integral estimates themselves. Commonly known as Richardson's extrapolation, this method calculates a more accurate third estimate using two initial integral estimates.
The estimates and errors associated with the multiple application trapezoidal rule can generally be expressed as follows.

Here. $I$ represents the value of the integral, $I(h)$ is the estimate from the $n$-segment application of the trapezoidal rule with a step size $h=(b-a)/n$, and $E(h)$ is the truncation error. If two separate estimates are made with step sizes ${h_1}$ and ${h_2}$, and the exact value of the error is know, then
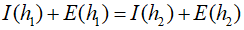
The error in the multiple application trapezoidal rule can be roughly expressed as follows.
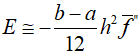
If we assume that ${\bar f^{''}}$, the function value, remains constant regardless of the step size, the ratio of the two errors can be degermined.
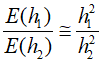
This allows for the term ${\bar f^{''}}$ to be eliminated from the equation. By doing this, we can utilize inherent information without prior knowledge of the function's second derivative.

By substituting this into the above formula, the calculation can be expressed as follows.
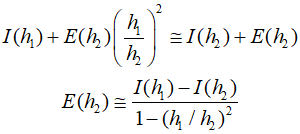
Therefore, the estimates of the truncation error were calculated using the integral estimates and their step sizes. Subsequently, the estimates can be subsitituted as follows.
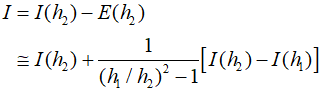
This involves combining two trapezoidal rule estimates with $O({h^2})$ error to obtain a new integral estimate with $O({h^4})$ error. In the special case where the step size is halved, it can be expressed as follows.
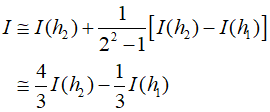
Thisapproach is a more heneral method for combining integrals to obtain improved estimates. In the special case based on the original trapezoidal estimates, where the step size is successively halved, the equation used for $O({h^6})$ accuracy can be expressed as follows.
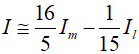
Here ${I_m}$ and ${I_l}$ represent the more accurate and less accurate estimates, respectively, Similarly, by combining the two results, an integral with $O({h^8})$ occuracy can be calculated.
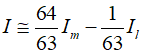
'Numerical Methods' 카테고리의 다른 글
| 162_Runge-Kutta Methods (0) | 2024.05.11 |
|---|---|
| 160_Simpson's 3/8 Rule (0) | 2024.05.08 |
| 159_Multiple SImpson's 1/3 Rule (0) | 2024.05.07 |
| 158_Simpson's Rules (0) | 2024.05.06 |
| 157_Multiple Trapezoidal Rule (0) | 2024.05.05 |