One method to enhance the accuracy of the trapezoidal rule, as explained the previous posting, involves dividing the interval into multiple segments and applying the method to each segment. Subsequently, by summing the area of each segment, the integral for the entire interval can be obtained. There are $n$ eqaully spaced reference points, thus it is assumed that there are $n$ segments of the same width.

If a $a$ and $b$ are represented as ${x_0}$ and ${x_n}$, respectively, the total integral can be expressed as follows.

When the trapezoidal rule is applied, it can be expressed as follows.

General form is
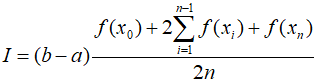
Since the sum of the coefficients of the numerator of $f(x)$ divided by $2n$ equals 1, the average height represents the weighted average of the function values. The error in the multiple application of the trapezoidal rule can be obtained by summing the individual errors of each segment.

Here, ${{f^{''}}({\xi _i})}$ represents the second derivative at point ${{\xi _i}}$ within segment $i$. This result can be simplified by estimating the average value of the second derivative over the entire interval, or by using the mean value.
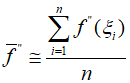
Therefore,
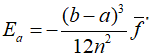
Using this method to solve an example that estimates the following integral.

Lets estimate the error using the trapezoidal rule with two intervals when $a$ is $0$ and $b$ is $0.8$. The correct integral value is $1.640533$. When $n=2$.


'Numerical Methods' 카테고리의 다른 글
| 159_Multiple SImpson's 1/3 Rule (0) | 2024.05.07 |
|---|---|
| 158_Simpson's Rules (0) | 2024.05.06 |
| 156_Trapezoidal Rule (0) | 2024.05.04 |
| 155_Least Squares Fit (0) | 2024.05.03 |
| 154_Cubic Splines (0) | 2024.05.02 |