Similarly to the trapezoidal rule, Simpson's rule can also imrpove results by dividing the integration interval into multiple segements of equal width.
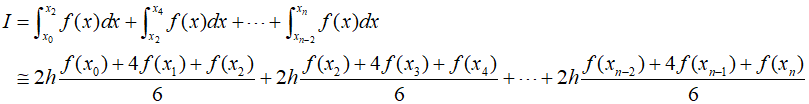
Therefore,

To implement this method, an even number of segments must be used, as the odd points represent the middle terms in each application and thus carry a weight of $4$. Even points are used commonly between adjacent segments and are thus counted twice. The error estimation for the multiple application of Simpson's rule, like the trapezoidal rule, can be obtained by summing the individual errors of each segment and averaging the derivatives.

Use this method to estimate the following integral when $n=4$.
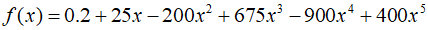
Set $a=0$ and $b=0.8$. The integral value in this case is $1.640533$.
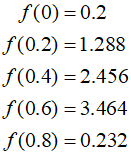
Applying the given formula, the calculation can be expressed as follows.

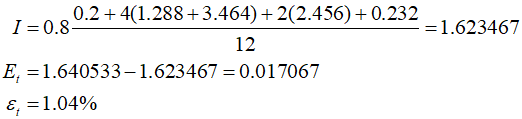
The estimated error can be expressed as follows.
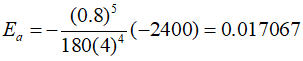
This example demenstrates that the multiple application version of Simpson's $1/3$ rule provides very accurate estimates. For this reason, it is oftern preferred over the trapezoidal rule in most fields due to its superior accuracy and is more widely used. However, as previously mentioned, it can only be applied when the values are equidistant, and it requires an even number of segments and an odd number of points, which are limitations.
'Numerical Methods' 카테고리의 다른 글
| 161_Richardson's Extrapolation (0) | 2024.05.09 |
|---|---|
| 160_Simpson's 3/8 Rule (0) | 2024.05.08 |
| 158_Simpson's Rules (0) | 2024.05.06 |
| 157_Multiple Trapezoidal Rule (0) | 2024.05.05 |
| 156_Trapezoidal Rule (0) | 2024.05.04 |