In a previous post, I theoretically covered the method for calculating the stiffness matrix of a tetrahedron. In this post, based on that theory, I aim to derive the stiffness matrix of a tetrahedron through an example. The given tetrahedral element is as follows.
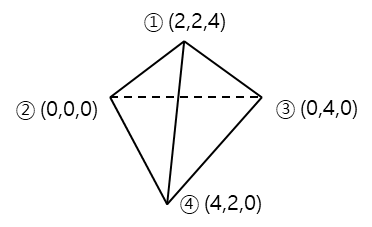
In the given element, $E = 200{\text{GPa}},\,v = 0.3$.
To calculate the element stiffness matrix first, it is necessary to determine the volume $V$ of the element and all $\alpha ,\beta ,\gamma $, and $\delta $ values. These can be calculated by substituting into the theoretical formulas derived in a previous post.
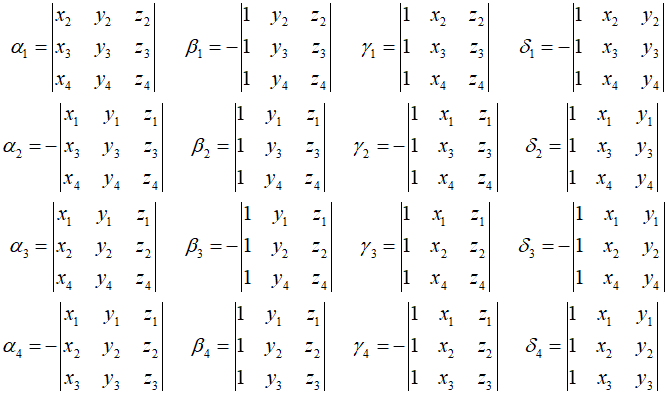
The calues can be determined by substituting the coordinates of the element.
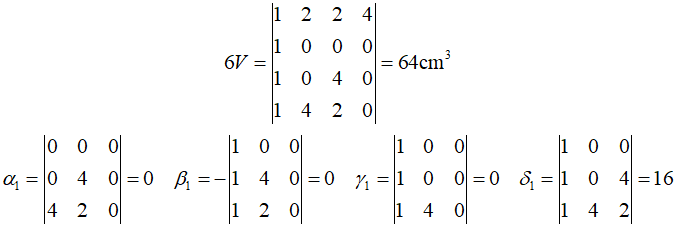
The remaining values can also be determined by substitution.
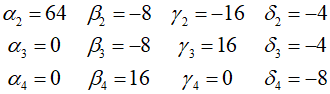
Next, the shape functions are determined.
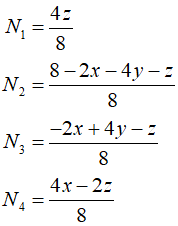
The $B$ matrix can be determined as follows.

By subsituting the values, four $B$ matrixs can be obtained as follows.

The matrix $[D]$ is

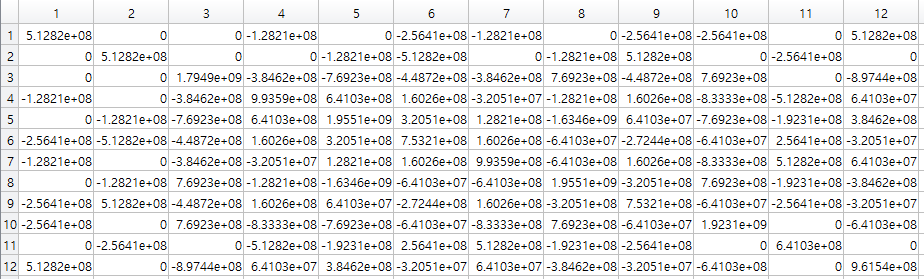
$B$ matrix is $\left[ {\left[ {{B_1}} \right]\left[ {{B_2}} \right]\left[ {{B_3}} \right]\left[ {{B_4}} \right]} \right]$, and stiffness matrix can be calculated through the following formula.

Due to the large and complx of the matrix, the calculation was performed using MATLAB, and the result is as follows.

'Finite Element Method' 카테고리의 다른 글
| 96_Heat Flux Example (0) | 2024.03.05 |
|---|---|
| 94_Two-Point Gaussian Integration (0) | 2024.03.03 |
| 93_Linear Plane Quadrilateral Example (0) | 2024.03.02 |
| 91_Plane Stress Example (0) | 2024.02.29 |
| 49_Heat Transfer with Mass Transport (0) | 2024.01.18 |