Although the total energy equation has been covered in a previous post, there's a section in another book that explains it in a more understandable manner, prompting me to write about the same topic again.
When considering the energy of compressible media in the Bernoulli equation, the total energy equation should be used instead of the mechanical energy equation. The total energy equation can be expressed as follows.

In comporessible fluids, density can vary with pressure and temperature, thus incoporating thermodynamics into energy considerations is essential. The equation represents the total energy change, including internal energy ($e$), kinetic energy ($U_j^2$), and potential energy($G$). This takes into account scenarios where contributions from molecular-dependent heat and momentum transfer are neglected and where the influence of gravity is considered negligible.
The energy equation for steady-state flow is as follows.
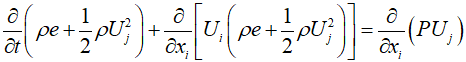
In the case of a fixed flow, where the time derivative terms are neglected, it can be stated as follows.

By neglecting the terms related to time and introducing enthalpy, which is the sum of internal energy and pressure energy, the energy equation for the steady flow of compressible fluids can be obtained. Consequently, the sum of enthalpy and kinetic energy is constant.
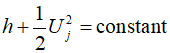
It is understood that the sum of the area-averaged enthalpy and the area-averaged kinetic energy per unit mass is constant in adiabatic flow, where viscosity is negligible and the influence of gravity can be ignored. Through this, the necessary equations for calculating the flow within a tube can be derived.

The sum of the area-averaged enthalpy of the flowing fluid and the area-averaged kinetic energy per unit mass of the fluid remains constant in the absence of viscosity and when the effects of gravity can be disregarded. Consequently, this leads to the derivation of equations for calculating the flow within flow conduits as follows.
Incompressible flow
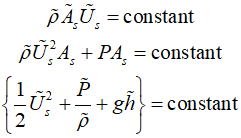
Compressible flow

'Fluid Dynamics' 카테고리의 다른 글
| 90_Momentum Equation (0) | 2024.02.28 |
|---|---|
| 89_Continuity Equation (0) | 2024.02.27 |
| 88_Bernoulli Equation (1) | 2024.02.26 |
| 87_Equation of Motion (0) | 2024.02.25 |
| 86_Newton's Second Law of Motion (0) | 2024.02.24 |