The continuity equation in fluid mechanics mathematically represents the principle of mass conservation within fluids. Physically, it asserts that the mass inflow and outflow through any given control volume remains constant over time. Therefore, the continuity equation is critical for analyzing fluid flow, applicable to both incompressible and compressible fluids alike.
In this post, I aim to explain the derivation process based on the differential form of the law of mass conservation for fluids. The differential form of mass conservation is as follows.
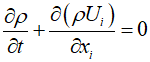
Where $\rho $ represents the density of the fluid, and ${U_i}$ denotes the $i$th component of the fluid velocity. Integrating this differential form over a control volume ${V_c}$ and applying the Gauss's integral theorem yields the following equation.
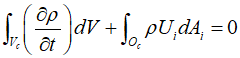
Where ${O_c}$ represents the outer surface of the control volume, and $d{A_i}$ denotes the surface element. The equation indicates that the rate of mass change within the control volume must equal the rate of mass entering or exiting through the control volume's surface. By interchanging the order of integration and differentiation with respect to the control volume, it can be expressed as follows.

The mass flux passing through the boundaries of the control volume is derived from the flow across the boundary surface using the divergence theorem and has the following relationship.
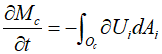
This indicates that the rate of total mass change within the control volume must equal the sum of mass flow passing through the control volume. In a steady state, where there is no change in mass within the control volume ($\frac{{\partial {M_c}}}{{\partial t}} = 0$), this means that the inflow and outflow must be equal. Applying this principle to a flow filament, the mass flow rate through all cross-sections must be consistent. In other words, the mass flow rate at any cross-section A must be equal to the mass flow rate at any other cross-section B.
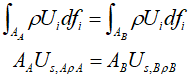
Where ${U_s}$ represent the velocity of the fluid flowing along the filament, and the equation demonstrates that the mass flow rates at two different points are equal. To apply this to fluid flows where the changes are not significant, it is necessary to perform an averaging of the continuity equation.
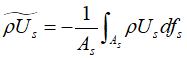
The equation represent the average of the product of the fluid's density and velocity ($\rho {U_s}$) for a specific cross-sectional area ${A_s}$, and is used to describe the mass flow. Here, the averaged values are utilized to express the conservation of mass in the fluid.
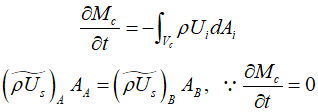
In steady-state flow, it means that the mass flow of fluid passing through one cross-section is the same as the mass flow through another cross-section. Using the averaged density($\tilde \rho $) and velocity (${\tilde U_s}$), it can be represented as follows.
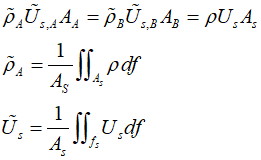
Using the equations, we can represent the changes in a fluid's relative velocity, density, and cross-sectional area as floows.

It indicates that the relative changes in the fluid's density, velocity, and cross-sectional area cancel each other out. When analyzing fluid flow with minimal changes, using these averaged values and relationships can simplify and solve the problem.
'Fluid Dynamics' 카테고리의 다른 글
| 92_Energy Equation(2) (1) | 2024.03.01 |
|---|---|
| 90_Momentum Equation (0) | 2024.02.28 |
| 88_Bernoulli Equation (1) | 2024.02.26 |
| 87_Equation of Motion (0) | 2024.02.25 |
| 86_Newton's Second Law of Motion (0) | 2024.02.24 |