In this post, I aim to explain the modifications of the momentum equation based on the stream tube theory used in fluid mechanics to solve flow problems. When analyzing fluid flow, the momentum equation can be used to determine the fluid's velocity, pressure, density, and other properties.
The basic form of the general momentum equation is as follows.
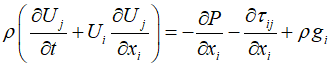
The equation represents the change in momentum of the fluid, including stress due to viscosity($\tau $) and gravity($g$). It is generally applicable at any point within the fluid. To apply the stream tube theory, the term for momentum transfer due to vicosity must be neglected, and the momentum equation must be modified considering the direction in which gravity acts.
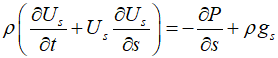
Where ${g_s} = - g\cos \alpha $ represents the component of gravitational acceleration in the direction of the stream tube, with $\cos \alpha $ based on the slope angle as $dz/ds$.

The momentum equation in the transverse direction of the stream tube, which is not along the direction of the stream tube but perpendicular to it, is as follows.
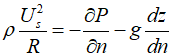
To integrate the momentum equation throught the control volume, starting from the Euler form of the momentum equation and neglecting the molecular momentum loss terms, it can be represented as follows.
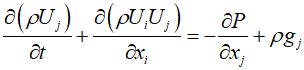
This allows for the analysis of fluid flow in a steady state.

Finally, consider the modifications of the momentum equation taking into account the conditions at the beginning and end of the stream tube. It addresses the flow conditions when considering or neglecting gravity, thereby determining the relationship between the fluid's velocity and pressure.

The momentum equation, among various other equations, can be usefully employed to analyze dynamic behaviors in situations of fluid flow.
'Fluid Dynamics' 카테고리의 다른 글
| 92_Energy Equation(2) (1) | 2024.03.01 |
|---|---|
| 89_Continuity Equation (0) | 2024.02.27 |
| 88_Bernoulli Equation (1) | 2024.02.26 |
| 87_Equation of Motion (0) | 2024.02.25 |
| 86_Newton's Second Law of Motion (0) | 2024.02.24 |