Graphs are commonly composed of a set of objects called nodes, which are connected by edges. Additionally, data can be associated with both nodes and edges. Therefore, graphs can represent many systems across various fields such as social networks, biology, and natural language processing.
In this post, we will explore how to apply deep learning to graph-structured data. This involves predicting the properties of nodes, the attributes of edges, or the characteristics of the entire graph. Graph neural networks typically define embedding vectors for each node, which are initialized with observed node attributes and then transformed through trainable layers. Additionally, learned embeddings related to edges and the entire graph can also be utilized.
Edges can be categorized into directed and undirected graphs based on the presence or absence of direction.
The explanation is based on a simple graph, where there is at most one edge between a pair of nodes, the graph is undirected, and there are no self-edges connecting a node to itself. A graph($G$) consists of a set of nodes or vertices, denoted by $V$, and a set of edges, denoted by $E$. The nodes are indexed as $n = 1, \cdots ,N$, and an edge from node $n$ to node $m$ is represented as $(n,m)$. If two nodes are connected by an edge, they are considered neighbors, and the set of all neighbors of node $n$ is denoted by $N(n)$.
The adjacency matrix, denoted as ${\text{A}}$, is used to specify the edges of a graph. If there are $N$ nodes in the graph, the adjacency matrix will have dimensions $N \times N$, with a 1 present at all locations where there is an edge from node $n$ to node $m$, and all other entires are 0. In the case of a graph with undirected edges, the adjacency matrix is symmetric. The existence of an edge from node $n$ to node $m$ implies that there is also an edge from node $m$ to node $n$, meaning that for all $n$ and $m$, ${A_{mn}} = {A_{nm}}$.
To mathematically represent the permutation of node labels, there is a permutation matrix ${\text{P}}$ that specifies a particular permutation of the node order. This matrix has the same size as the adjacency matrix, with each row containing a single 1, each column also contatning a single 1, and all other elements being 0. Let's consider a permutation from $\left( {{\text{A,B,C,D,E}}} \right) \to \left( {{\text{C,E,A,D,B}}} \right)$. The permutation matrix would have the following form.

The permutation function $\pi ( \cdot )$, which maps $n$ to $m = \pi (n)$, can be represented as follows.

When rearranging the node labeling of a graph, the effect on the corresponding node data matrix ${\text{X}}$ involves permuting the rows according to $\pi ( \cdot )$, which can be achieved by linearly multiplying by the permutation matrix ${\text{P}}$.

For the adjacency matrix, since both rows and columns are permuted, a new adjacency matrix can be generated using the following formula
To apply deep learning to graph structures, it's necessary to assign an order to the nodes to represent the graph structure in numerical form. However, the chosen specific order is arbitrary, so it must be ensured that all global features do not depend on a particular order. In other words, the network's predictions must be invariant to the rearrangement of node labels.
Here, $y$ represents the output of the network, and for predictions related to individual nodes, the same rearrangement should apply. Therefore, a specific prediction must always be associated with the same node, regardless of the choice of order.
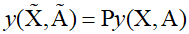
'Deep Learning' 카테고리의 다른 글
| 72_Generative Adversarial Networks (1) | 2024.02.10 |
|---|---|
| 71_Graph Convolutional Network (0) | 2024.02.09 |
| 69_Convolutional Filter (0) | 2024.02.07 |
| 68_Residual Connection (0) | 2024.02.06 |
| 67_Automatic Differentiation (1) | 2024.02.05 |