In a previous post(62_Gradient Information), we discussed the parameter known as the learning rate($\eta $) in the Stochastic Gradient Descent algorithm. $\eta $ is a parameter that needs to be set, and if its value is too small, learning proceeds slowly. On the other hand, if $\eta $ is too large, it can lead to very unstable training of the model. Therefore, setting an appropriate value for $\eta $ is improtant. Finding this value through trial and error can be very time-consuming, so it is common to start with a larger value $\eta $ and gradually reduce it as learning progresses, using what is known as a learning rate schedule.
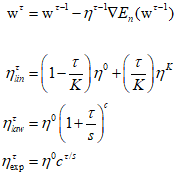
The above formula shows learning rate schedules for linear, power law, and exponential decay. Here, $\eta $ decreases linearly over $K$ steps, and then remains constant at ${\eta ^K}$. Appropriate values for the hyperparameters ${\eta ^0},{\eta ^K},K,S$, and $c$ must be determined empirically.
And these learning rate values are automatically adjusted during training, hence a variety of algorithms are widely used. Among them, AdaGrad(Adaptive Gradient) uses the cumulative sum of the squares of all the derivatives calculated for a given parameter to decrease each learning rate parameter over time. As a result, paramters with higher curvature decrease the fastest.
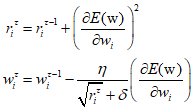
Where $\eta $ is the learning rate parameter, $\delta $ is a very small value close to 0 for numerical stability, and $E({\text{w}})$ is the error function for a specific mini-batch. The problem with AdaGrad is that it accumulates squared gradients from the beginning of training, resulting in very small weight updates and consequently very slow learning later on. There fore, the RMSProp algorithm, an acronym for Root Mean Square Propagation, replaces the sum of squared gradients in AdaGrad with an exponentially weighted average.
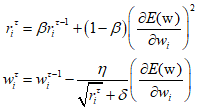
Where $0 < \beta < 1$, typically set to 0.9. If RMSProp is combined with momentum, it becomes the Adam optimization method, derived from 'Adaptive moments'. Adam stores momentum separately for each parameter and uses an update method that emplys exponentially weighted moving averages for both the gradient and squared gradient.
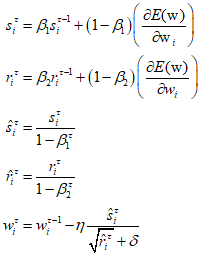
Where $1/\left( {1 - \beta _1^\tau } \right)$ and $1/\left( {1 - \beta _2^\tau } \right)$ are factors that correct the bias intorduced by initializing $s_i^0$ and $r_i^0$ to 0. Common values for the weight parameters are ${\beta _1} = 0.9$ and ${\beta _2} = 0.99$. Adam is one of the most widely used learning algorithms in deep learning and proceeds in the following steps.

'Deep Learning' 카테고리의 다른 글
| 65_Backpropagation (0) | 2024.02.03 |
|---|---|
| 64_Normalization (0) | 2024.02.02 |
| 62_Gradient Information (0) | 2024.01.31 |
| 61_Gradient Descent (0) | 2024.01.30 |
| 60_Multilayer Networks and Activation Function (0) | 2024.01.29 |