The main idea of neural networks is to select basis functions with learnable parameters and adjust these parameters to minimize an error function defined over all parameters in the model. To achieve this, gradient-based optimization method, like gradient descent, are typically used to optimize the entire model.
For example, in a basic neural network model with two layers of learnable parameters, a linear combination of input variables can be constructed as follows.

Where, the superscript $(1)$ indicates that the parameters are in the first layer of the network, $w_{ji}^{(1)}$ represents the weights, $w_{j0}^{(1)}$ is the bias, and $a_j^{(1)}$ is the pre-activation. Each ${a_j}$ can be transformes using a differentiable nonlinear activation function as follows.
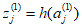
The above equation represents the output of the basis functions, which can be expressed as a linear combination.

Where $k = 1, \cdots ,K$, and $K$ is the total number of outputs. Here, an appropriate output activation function is used to obtain the set of outputs.
If ${x_0}=1$ in the linear combination $a_j^{(1)}$, then it takes the following form.

Therefore, as the bias of the second layer can be transformed into the weights of the second layer, the overall network function is as follows.
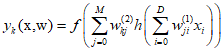
The representation can be further simplified using vector and matrix notation.

Additionally, I would like to briefly mention activation functions. Typically, activation functions are applied uniformly to all hidden layers of the network and must be differentiable.
The commonly used forms of differentiable nonlinear functions are as follows.
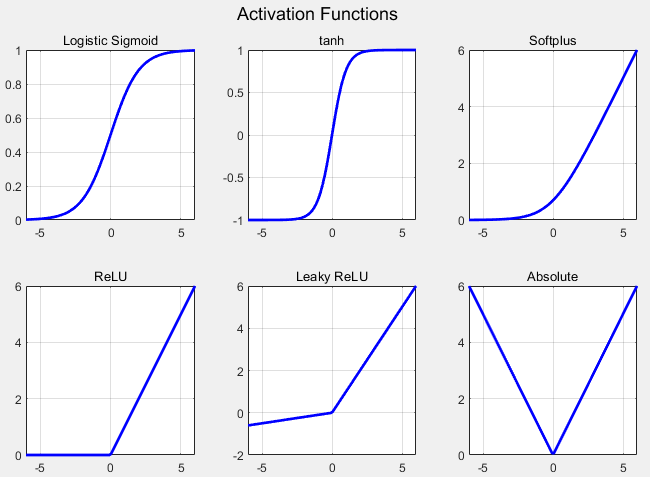
Describing the characteristics of each activation function.
The Logistic Sigmoid has an output range limited between 0 and 1, making it suitable for modeling probability values and for training using gradient descent. However, it can suffer from the gradient vanishing problem when input values are significantly positive or negative.
Tanh is similar to the sigmoid but has an output range from -1 to 1, making it suitable for learning the weights of a neural network. Like the sigmoid, it can also face the gradient vanishing issue.
Softplus increases in a log function form when the input is positive, and its output is always positive. However, as the graph increases indefinitely, large values can impact performance.
ReLU outputs the input value directly if it is positive and outputs 0 if it is negative. It is computationally efficient and converges quickly during training due to a constant gradient in the positive region. However, it can face the gradient vanishing problem with negative input values.
Leaky ReLU is similar to ReLU but uses a small, positive linear function for negative input values to mitigate the gradient vanishing problem.
Absolute outputs the absolute value of the input, with the gradient being 1 or -1 depending on the sign of the input.
Among these, the most commonly used activation function is ReLU
'Deep Learning' 카테고리의 다른 글
| 62_Gradient Information (0) | 2024.01.31 |
|---|---|
| 61_Gradient Descent (0) | 2024.01.30 |
| 59_Generative Classifiers(2) (1) | 2024.01.28 |
| 58_Generative Classifiers (0) | 2024.01.27 |
| 57_Single Layer Classification (1) | 2024.01.26 |