Continuing with additional content following the last post.
If there is data composed of a dataset and corresponding class labels, a parametric form for the class-conditional densities can be specified. Through this, the values of the parameters can be determined using maximum likelihood.
First, let's assume there are two classes. Each class has a Gaussian class-conditional density with a shared covariance matrix, and the dataset is $\{ {{\text{x}}_n},{t_n}\} $. Here, ${t_n}=1$ represents ${C_1}$, and ${t_n}=2$ represents ${C_2}$. The prior class probabilities are $p({C_1}) = \pi $ and $p({C_2}) = 1 - \pi $. Since in class ${C_1}$, for a data point ${{\text{x}}_n}$, ${t_n}=1$, it can be represented as follows.
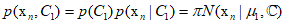
In class ${C_2}$, ${t_n}=0$.

Therefore, the likelihood function is as follows.

Where ${\text{t}} = {({t_1}, \cdots {t_N})^T}$, and as previously explained, it is convenient to take the log to maximize the log likelihood function. In the above function, terms dependent on $\pi$ can be organized as follows.
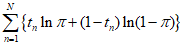
setting the derivative to 0.

Where the total number of data points belonging to classes ${C_1}$ and ${C_2}$ are ${N_1}$ and ${N_2}$, respectively. Therefore, the maximum likelihood estimate for $\pi$ is the proportion of data points in ${C_1}$, meaning the maximum likelihood estimate for the prior probability of class ${C_k}$ is the proportion of training set points assigned to that class.
Next, organizing the terms dependent on $\mu $ yields the following.

Similarly, setting the derivative to 0 results in the following.

Finally, considering the maximum likelihood solution for the shared coveriance matrix ${\Bbb C}$ results in the following.
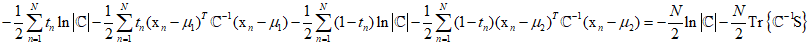
Therefore,
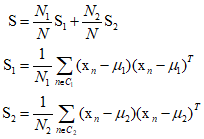
From the results of the maximum likelihood values for the Gaussian distribution, we can see that ${\Bbb C} = {\text{S}}$, which represents the weighted average of the covariance matrices for each class.
'Deep Learning' 카테고리의 다른 글
| 61_Gradient Descent (0) | 2024.01.30 |
|---|---|
| 60_Multilayer Networks and Activation Function (0) | 2024.01.29 |
| 58_Generative Classifiers (0) | 2024.01.27 |
| 57_Single Layer Classification (1) | 2024.01.26 |
| 56_Sequential Learning (1) | 2024.01.25 |