In this post, we will study classificaion problems that can be represented with single-layer neural networks. I would like to emphasize again that I am studing this based on C hris Bishop's "Deep Learning - Foundations and Concepts"
Classification aims to assign an input vector $x$ to one of $K$ discrete classes, ${C_k}$. Consequently, the input space is divided into decision regions, and these boundaries or surfaces are referred to as decision surfaces.
The content we will study focuses on linear models where the decision surfaces are defined by linear functions of the input vector $x$ and we'll explore this mathematically.
In this post, we will discuss methods of creating a discriminant function to directly assign input vectors $x$ to classes.
A linear discriminant function can be simply represented through a linear function of the input vector.
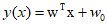
Where ${\text{w}}$ is the weight vector, and ${w_0}$ is the bias. If the input vector $x$ satisfies $y(x) > 0$, it is assigned to ${C_1}$, otherwise to ${C_2}$. Therefore, the decision boundary is $y(x)=0$, which represents a $D-1$ dimensional hyperplane in $D$ dimensional space.
If $x$ is a point on the decision surface, then $y(x)=0$, and the normal distance from the origin to the decision surface is as follows.

Therefore, the bias paramter ${w_0}$ determines the position of the decision surface, and the value of $y(x)$ represents the perpendicular distance $\tau$ from the point $x$ to the decision surface.
When an arbitrary point $x$ exists, if the orthogonal projection on $x$ is denoted as ${{\text{x}}_ \bot }$, the following equation holds true.
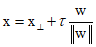
When extending to cases where $K$ is gerater than 2, ambiguous regions can be created. For example, if the decision boundaries are composed of three lines that are neither orthogonal nor parallel, a total of four regions are formed. To avoid this, we can consider $K$ discriminant functions in the form of the following linear functions.

If ${y_k}({\text{x}}) > {y_j}({\text{x}})$ for all $j \ne k$, then the point $x$ is assigned to ${C_k}$. The decision boundary between ${C_k}$ and ${C_j}$ is defined by ${y_k}({\text{x}}) = {y_j}({\text{x}})$. Therefore, hyperplanes can be defined as follows.
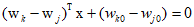
Using such discriminant functions ensures that the decision regions are always singly connected. Therefore, for any two points ${{\text{x}}_{\text{A}}}$, ${{\text{x}}_{\text{B}}}$ in the decision region ${R_k}$, all points ${\hat{\text{x}}}$ on the line connecting ${{\text{x}}_{\text{A}}}$ and ${{\text{x}}_{\text{B}}}$ can be represented as follows.
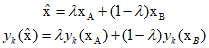
Since both ${{\text{x}}_{\text{A}}}$ and ${{\text{x}}_{\text{B}}}$ are within ${R_k}$, it holds that ${y_k}({{\text{x}}_{\text{A}}}) > {y_j}({{\text{x}}_{\text{A}}})$ and ${y_k}({{\text{x}}_{\text{B}}}) > {y_j}({{\text{x}}_{\text{B}}})$. Furthermore, since ${y_k}({\hat{\text{x}}}) > {y_j}({\hat{\text{x}}})$ for all $j \ne k$, ${\hat{\text{x}}}$ also exists within ${R_k}$. Therefore, ${R_k}$ is singly connected and convex.
ref : Chris Bishop's "Deep Learning - Foundations and Concepts"
'Deep Learning' 카테고리의 다른 글
| 59_Generative Classifiers(2) (1) | 2024.01.28 |
|---|---|
| 58_Generative Classifiers (0) | 2024.01.27 |
| 56_Sequential Learning (1) | 2024.01.25 |
| 55_Likelihood Function (0) | 2024.01.24 |
| 54_Linear Regression (0) | 2024.01.23 |