Consider an infinitesimal element of dimensions $dx$, $dy$ and $dz$ in a three-dimensional Cartesian coordinate system, subjected to normal and shear stresses.
The normal stresses acting perpendicularly on the surfaces are denoted as ${\sigma _x}$, ${\sigma _y}$ and ${\sigma _z}$, while the shear stresses acting within the planes are represented as ${\tau _{xy}}$, ${\tau _{yz}}$ and ${\tau _{zx}}$.
Due to the moment equilibrium of the element, the following relationship holds.
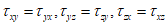
Additionally, with three independent shear stresses and three normal stresses, the strain-displacement releationship of the element can be represented as follows.

Where $u$, $v$ and $w$ are the displacements in the $x$, $y$ and $z$ directions, respectively, and the shear stresses are as follows.
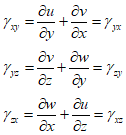
The stress and strain can be represented in matrix form as follows.
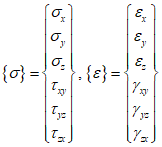
The fundamental stress-strain relationship for linear elasticity in isotropic materials can be represented as follows.

$\sigma $ and $\varepsilon $ represent the stress and strin vectors, respectively. The $D$ matrix defines the relationship between stress and strain, allowing for the calculation of this relationship and the modeling of mechanical properties.
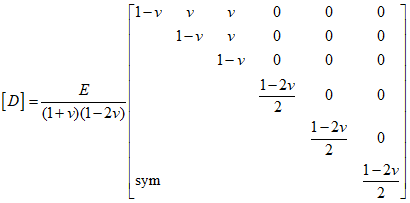
'Finite Element Method' 카테고리의 다른 글
| 42_One-Dimensional Heat Conduction (1) | 2024.01.11 |
|---|---|
| 41_Tetrahedral Element (1) | 2024.01.10 |
| 39_High Order Example (0) | 2024.01.08 |
| 38_High Order Shape Function (0) | 2024.01.07 |
| 37_Element Stress (1) | 2024.01.06 |