In the last post, I discussed the stress-strain of hexahedral elements, and in this post, I'll calculate the stiffness matrix of tetrahedral elements.
Numbering each of the four nodes of the tetrahedron, the displacement at each node can be represented as follows.
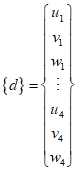
Since there are three degress of freedom per node, there are a total of 12 degrees of freedom.
The element displacement functions $u$, $v$ and $w$ are linear along each edge, with only two existing per edge, and are also linear in each plane.
Therefore, the linear displacement function can be represented as follows.
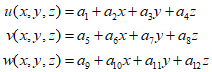
${a_i}$ can be expressed using known node coordinates and unknown node displacements as follows.
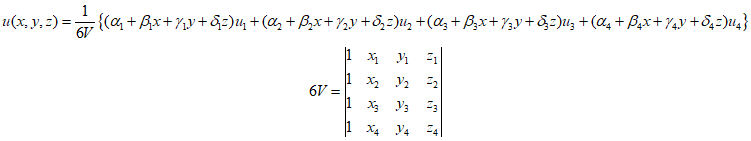
In the above equation, the coefficients ${\alpha _i}$, ${\beta _i}$, ${\gamma _i}$ and ${\delta _i}$ are as follows.
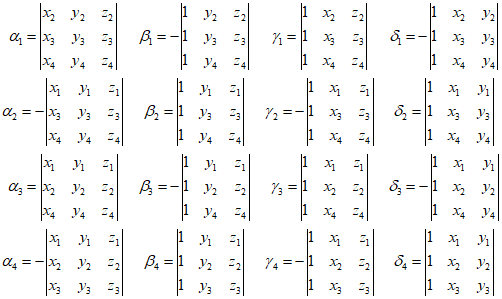
Furthermore, the displacement for $u$ can also be expressed as follows, and the same applies for $v$ and $w$.
This allows for the representation of the shape function and the expression for the known node displacements.
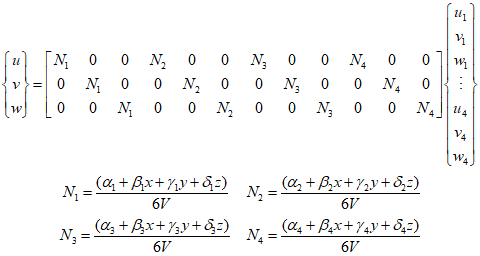
In three dimensions, the stress of the element can be represented as follows.
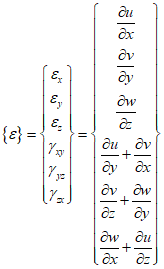
Therefore, the following equation can be obtained.
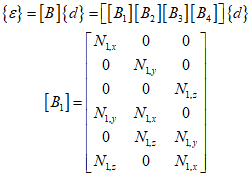
Where, the subscript comma denotes differentiation with respect to the following variable. ${B_2}$, ${B_3}$ and ${B_4}$ can also be represented similarly.
Furthermore, by substituting the shape functions, it can be expressed as follows.
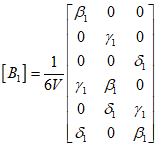
Therefore, the stiffness matrix, body force, and surface force can be represented as follows.

'Finite Element Method' 카테고리의 다른 글
| 43_1-D Heat Transfer Finite Element Formulation (0) | 2024.01.12 |
|---|---|
| 42_One-Dimensional Heat Conduction (1) | 2024.01.11 |
| 40_3-Dimensional Stress and Strain (0) | 2024.01.09 |
| 39_High Order Example (0) | 2024.01.08 |
| 38_High Order Shape Function (0) | 2024.01.07 |