As explained in the previous post, an $n$th degree polynomial can be expressed as follows.
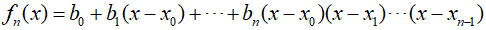
As with linear and quadratic interpolation, data points can be used to calculate the coefficients ${b_0},{b_1}, \cdots ,{b_n}$, and for an $n$th degree polynomial, $n+1$ data points are required. These data points can be used to calculated the coefficients through the equation below.
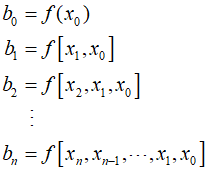
Here, the function inside the brackets represents the finite divided differences. For example, the first finite difference is typically expressed as follows.

The second finite difference, which represents the difference of the first differences, is expressed as follows.
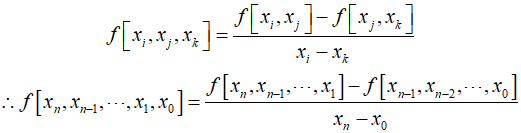
These differences can be used to evaluate the coefficients of the equation, and using them, an interpolation polynomial can be derived.
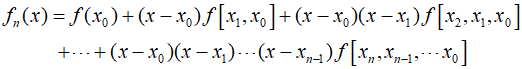
This is called Newton's divided-difference interpolating polynomial. The data points do not need to be equidistant, and the $x$-values of the points do not need to be in ascending order. In other words, higher-order differences are calculated by taking the difference of lower-order differences. Let's solve an example estimating the value of $\ln 2$ using this method. In the previous example, three data points were used for estimation. This time, by adding ${x_3} = 5$, I'll use Newton's third-degree interpolating polynomial to estimate the value.

The first divided differences is as follows.
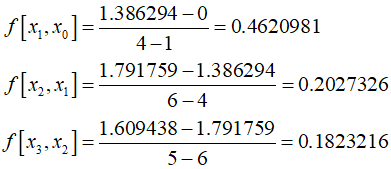
The second divided differences is

And the third is

The results obtained represent the coefficients of the equations. Therefore, they can be summarized as follows.

Using this, the calculation results in $0.6287686$, which shows an error of 9.3% compared to the original value.
'Numerical Methods' 카테고리의 다른 글
| 152_Derivation of Cubic Splines (0) | 2024.04.30 |
|---|---|
| 151_Lagrange Interpolation Polynomials (0) | 2024.04.29 |
| 149_Quadratic Interpolation (0) | 2024.04.27 |
| 148_Linear Interpolation (0) | 2024.04.26 |
| 147_Nonlinear Regression (1) | 2024.04.25 |