In engineering problems, there are instances when it's necessary to estimate values between data points. The most commonly used method for this purpose is polynomial interpolation. Typically, an $n$-th degree polynomial is expressed as follows.
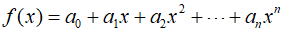
For $n+1$ data points, there exists only one $n$-th degree polynomial that passes through all these points, just as there is only one straight line that connects two points, and only one parabola that connects three points. Polynomial interpolation is the process of determining this unique $n$-th degree polynomial that fits $n+1$ data points.
In this post, I'll discuss the Newton polynomial, a method for representing such polynomials.
Newton's divided-difference interpolating polynomial is one of the most widely used and useful forms of polynomial interpolation.
The simplest form of interpolation that connects two data points with a straight line is called linear interpolation. It can be expressed as follows.
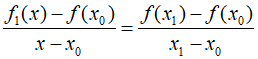
By rearranging, we can derive the formula for linear interpolation as follows.
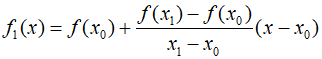
Here ${f_1}(x)$ indicates that this is a first-order interpolating polynomial. It is represented very simply.
To estimate the value of $\ln 2$ using linear interpolation, we'll interpolate between $\ln 1 = 0$ and $\ln 6 = 1.791759$. Using the linear interpolation formula, we can expressed as follows.
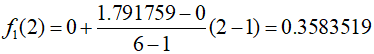
The result shows an error of about 48% compared to the actual value of $\ln 2 = 0.6931472$. So, recalculate using a smaller interval between $\ln 1 = 0$ and $\ln 4 = 1.386294$ to improve accuracy.
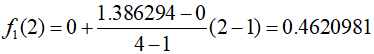
The result show an error of about 33.3% compared to the actual value. This demonstrates that using a smaller interval for interpolation can reduce the error.
'Numerical Methods' 카테고리의 다른 글
| 150_Newton's Interpolation Polynomials (0) | 2024.04.28 |
|---|---|
| 149_Quadratic Interpolation (0) | 2024.04.27 |
| 147_Nonlinear Regression (1) | 2024.04.25 |
| 146_Polynomial Regression (0) | 2024.04.24 |
| 145_Newton's Method (0) | 2024.04.23 |