There exists a procedure for deriving the equation of a line using the least squares criterion. However, some engineering data, while showing clear patterns, often cannot be accurately represented by a straight line. In such cases, using a curve rather than a line is more appropriate to represent the data. Therefore, transformations are used to represent curves or polynomial regression is applied to fit polynomials to the data.
The least squares procedure can be easily extended to fit data to higher-degree polynomials. For example, consider the following second-degree polynomial, also known as a quadratic polynomial.
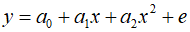
In this case, the sum of the squares of the residuals can be expressed as follows.

The derivatives of the above expression yields the following.

Set these equations to zero and rearrange them to generate a set of normal equations as follows.

The above three equations all involve summations from 1 to $n$, where ${a_0}$, ${a_1}$, and ${a_2}$ are the unknowns in a set of three linear equations. The coefficients of these unknowns can be directly calculated from the data.
In such cases, solving the problem of determining a least squares second-degree polynomial is equivalent to solving these three simultaneous linear equations. This approach can be extended to fit higher-degree polynomials, such as an $m$-th degree polynomial, as follows.

Therefore, determining the coefficients for an $m$-th degree polynomial involves solving $m+1$ simultaneous linear equations. In such scenarios, the standard error can be defined as follows.
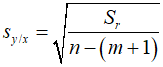
Here, ${S_r}$ represents the sum of the squares of the residuals, and $n-(m+1)$ is the number of degrees of freedom, where $n$ is the number of data points and $m$ is the degree of the polynomial. Additionally, the coefficient of determination for polynomial regression can be calculated as follows.
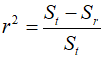
'Numerical Methods' 카테고리의 다른 글
| 148_Linear Interpolation (0) | 2024.04.26 |
|---|---|
| 147_Nonlinear Regression (1) | 2024.04.25 |
| 145_Newton's Method (0) | 2024.04.23 |
| 144_Parabolic Interpolation (0) | 2024.04.22 |
| 143_Golden-Section Example (0) | 2024.04.21 |