The Newton-Raphson method is a technique for finding the roots of $x$ where $f(x)=0$. This method can be summarized as follows.

A similar approach can be used to find the minimum or maximum values of $f(x)$. To do this, a new function is defined.
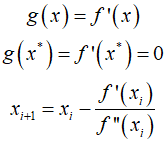
This method, similar to the Newton-Raphson approach, is an open method, so it does not requre initial estimates that bracket the optimum. Additionally, to ensure convergence towards the desired result, it's necessary to verify that the second derivative has the correct sign.
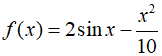
Similarly, let's proceed with an example using the same function, setting the initial estimate ${x_0}$ at $2.5$. first, calculate the first derivative and the second derivative of the function.

By substituting these into the formula, the calculation would proceed as follows.

Substitute the initial estimate into the equations to perform the calculation.
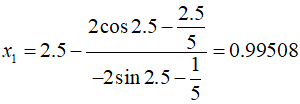
At this time, the function value is $1.57859$. The second iteration proceeds as follows.
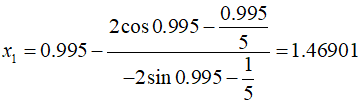
At this point, the function value is $1.77385$. This process should be repeated through further iterations. It can be easily implemented in MATLAB.
f = @(x) 2*sin(x)-(x^2)/10;
grad = @(x) 2*cos(x) - x/5;
hess = @(x) -2*sin(x) - 1/5;
x = 2.5;
maxiter = 5;
for i = 1:maxiter
H = hess(x);
G = grad(x);
x = x-H\G;
end
disp(x)
The result in this case is $1.4276$. While the Newton method works well in some cases, it is not practical when derivatives are difficult to compue. In this example, because the derivatives and second derivatives could be easily calculated, the computation was straightforward.
Moreover, this method is heavily influenced by the characteristics of the function and the initial estimates. It might not always converge, so it generally used when it is known that initial estimate is close to the optimum.
'Numerical Methods' 카테고리의 다른 글
| 147_Nonlinear Regression (1) | 2024.04.25 |
|---|---|
| 146_Polynomial Regression (0) | 2024.04.24 |
| 144_Parabolic Interpolation (0) | 2024.04.22 |
| 143_Golden-Section Example (0) | 2024.04.21 |
| 142_Golden-Section Search (0) | 2024.04.20 |