Parabolic interpolation leverages the existence of a single quadratic polynomial or parabola that connects three points, similar to how two points define a line. Therefore, if there are three points that collectively include an extremum, a parabola can be fitted to these points. Then, by differentiating this parabola and setting the derivative to zero, the optimal $x$ estimate can be found.
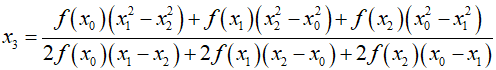
Here, ${x_0}, {x_1}$, and ${x_2}$ are initial estimates, and ${x_3}$ is the value of $x$ corresponding to the new estimate. After generating the new point, the preciously used points are reassigned sequentially for the next iteration. Alternatively, a bracketing approach similar to the bisection method or golden-section search can be used.

Solve the same example as in the previous post, this time using parabolic interpolation to find the maximum value. Set ${x_0}=0, {x_1}=1$, and ${x_2}=4$. First, calculate the function values for each of these initial estimates.
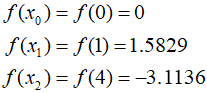
Substitute these values into the equation provided above.
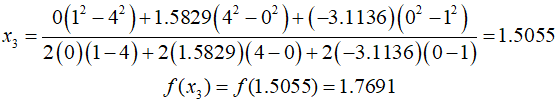
Next, use a method similar to the golden-section search to decide which point to discard. If the function value at the new point is greater than at the middle point ${x_1}$ and the new $x$ value is to the right of the middle point, the lower estimate ${x_0}$ is discarded. Therefore, the iteration proceeds as follows.
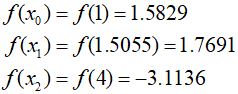
Substitute these values into the equation provided above.

Implement this algorithm using MATLAB and perform five iterations.
f = @(x) 2*sin(x)-(x^2)/10;
x0 = 0;
x1 = 1;
x2 = 4;
for a = 0:4
fx0 = f(x0);
fx1 = f(x1);
fx2 = f(x2);
num = fx0*(x1^2-x2^2)+fx1*(x2^2-x0^2)+fx2*(x0^2-x1^2);
den = 2*fx0*(x1-x2)+2*fx1*(x2-x0)+2*fx2*(x0-x1);
x3 = num/den;
if x0<x3 && x3<x1
x2 = x1;
x1 = x3;
elseif x1<x3 && x3<x2
x0 = x1;
x1 = x3;
elseif x2<x3
x2 = x3;
end
y = f(x3);
end
fprintf("x = %.4f\n", x3);
fprintf("y = %.4f\n", y);
Without delving deep into the intricaces and despite the potential for errors due to the simplicity of the approach, when executed, the result is $x=1.4275$ with a function value of $1.7757$.
'Numerical Methods' 카테고리의 다른 글
| 146_Polynomial Regression (0) | 2024.04.24 |
|---|---|
| 145_Newton's Method (0) | 2024.04.23 |
| 143_Golden-Section Example (0) | 2024.04.21 |
| 142_Golden-Section Search (0) | 2024.04.20 |
| 141_Gauss-Seidel Method (1) | 2024.04.19 |