Single-variable optimization problems aim to find the maximum or minimum value, that is, the extremum of $f(x)$. The golden-section search is a simple and versatile single-variable search technique.
Similarly, the bisection method relies on defining an interval with a lower estimate(${x_l}$) and an upper estimate(${x_u}$) that includes a single root. The presence of a root within these bounds is determined by checking if $f({x_l})$ and $f({x_u})$ habe opposite signs. Then, the midpoint of this interval is used to estimate the root.
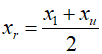
In the bisection method, the value of ${x_l}$ or ${x_u}$ that has the same sign as $f({x_r})$ is replaced, streamlining the interval toward the root. This approach has the advantage of replacing one of the interval's boundaries with the new value.
Focusing on finding a maximum or minimum value, we can start similarly to the bisection method by defining an interval that must contain a single extremum. Here, ${x_l}$ and ${x_u}$ represent the lower and upper bounds of this interval, respectively. Unlike the bisection method, which uses the midpoint primarily, finding an extremum within an interval involves using three function values, thus necessitating the selection of an additional point within the interval, followed by a fourth point. This setup allows for comparison of values to determine whether the maximum or minimum occurred in the first set of three points or in the last three.
The key to making this approach efficient lies in correctly selecting the midpoint. Like the bisection method, the goal is to minimize function evaluations, which can be achieved by replacing old values with new ones. This can be accomplished by setting the following two conditions.

The first condition ensures that the sum of the lengths of the two subintervals equals the original interval length, maintaining the integrity of the range being considered. The second condition requires that the proportions of these subintervals' lengths remain consistent, promoting even exploration within the defined interval.
Simplifying the above conditions, the expressions can be organized as follows.

If the reciprocal is taken and set as $R = {l_2}/{l_1}$, then it can be expressed as follows.

This value is known as the golden ratio. It is a critical element of the golden-section search method we are conceptually developing, which facilitates efficient identification of the optimum point. As previously mentioned, this method starts with two initial estimates, ${x_l}$ and ${x_u}$, that bracket a single local extremum of $f(x)$. Next, two internal points, ${x_1}$ and ${x_2}$, are chosen according to the golden ratio.

At thes point two internal points, the function is evaluated, leading to one of two possible outcomes.
If $f({x_1}) < f({x_2})$, then ${x_2}$ becomes the new ${x_l}$ for the next iteration. Conversly, if $f({x_2}) < f({x_1})$, then ${x_1}$ becomes the new ${x_u}$. Since the original ${x_1}$ and ${x_2}$ were chosen using the golden ratio, there is no need to recalculate all function values for the next iteration, which is a major advantage of the golden-section search. That is, the new value of $f({x_2})$ may already be the same as the previous function value at ${x_1}$, thus no new calculation is needed. Therefore, only the new ${x_1}$ needs to be determined, which can be calculated using the same ratio as before.

'Numerical Methods' 카테고리의 다른 글
| 144_Parabolic Interpolation (0) | 2024.04.22 |
|---|---|
| 143_Golden-Section Example (0) | 2024.04.21 |
| 141_Gauss-Seidel Method (1) | 2024.04.19 |
| 140_Cholesky Decomposition (0) | 2024.04.18 |
| 139_Thomas Algorithm (0) | 2024.04.17 |