In this post, I'll explore an example of finding the roots of a plynomial using Bairstow's method, as previously explained in an earlier post.

The initial values for $r$ and $s$ are set to $-1$, and ${\varepsilon _s} = 1\% $.
Similar to conventional synthetic division, recursive relations are used to perform the division by the quadratic factor, as follows.

Therefore, the simultaneous equations to find $\Delta r$ and $\Delta s$ are as follows.
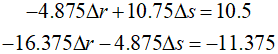
By solving the above simulaneous equations, we find that $\Delta r = 0.3558$ and $\Delta s = 1.1381$. Therefore, the initial estimates can be adjusted as follows.

The approximation error is calculated as follows.

Subsequently, repeat the calculations using the revised values of $r$ and $s$.

Therefore,

Since $\Delta r = 0.1331$ and $\Delta s = 0.3316$, the root estimates can be adjusted as follows.
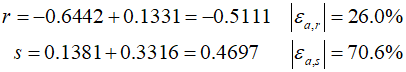
Continuing with such iterative calculations, after four iterations, the value of $r$ becomes $-0.5$ and $s$ becomes $0.5$. These values can then be used to calculate the roots.
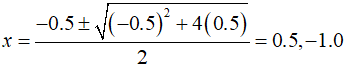
Here, the quotient is a cubic equation.
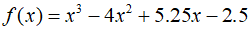
Apply Bairstow's method to this polynomial using the initial estimates of $r$ and $s$ obtained from the previous steps. After a total of five iterations, the estimated values of $r=2$ and $s=-1.249$ can be obtained, exabling further calculations.

'Numerical Methods' 카테고리의 다른 글
| 139_Thomas Algorithm (0) | 2024.04.17 |
|---|---|
| 138_Naive Gauss Elimination (0) | 2024.04.16 |
| 136_Bairstow's Method (0) | 2024.04.14 |
| 135_Muller's Method Example (0) | 2024.04.13 |
| 134_Muller's Method (0) | 2024.04.12 |