Gaussian elimination is one of the most fundamental algorithms for systematically eliminating unknowns and substituting in a set of equations. In this post, I'll explore Naive Gauss elimination through a simple example. Since it's a straightforward example and a basic algorithm, the explanation will be concise.
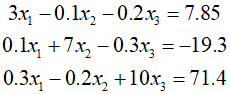
First, we go through the forward elimination process. We make the coefficients of ${x_1}$ in the first and second equations the same, then subtract one equation from the other to eliminate the ${x_1}$ term.

Similarly, multiply the first equation by 0.1 and subtract it from the fhird equation to eliminate the ${x_1}$ term. Consequently, this can be represented as follows.
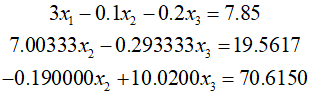
To complete the forward elimination process, the ${x_2}$ term in the third equation needs to be eliminated. By multiplying the second equation by a specific value and subtracting it from the third equation, the ${x_2}$ term is removed, and the system is reduced to an upper triangular form.
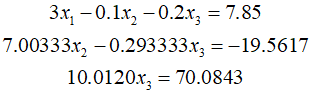
Can solve the equations using back substitution. ${x_3}$ can be determined as follows.

Therefore, the second equation is as follows.
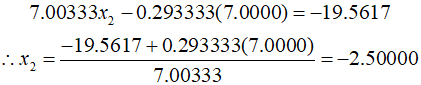
Therefore, by substituting ${x_2}$ and ${x_3}$ into the first equation, ${x_1}$ can be calculated.
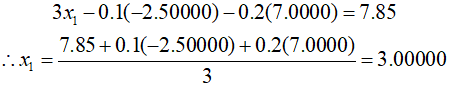
Thus, ${x_1} = 3,\,{x_2} = - 2.5,\,\,{\text{and }}{x_3} = 7$. To verify this, substituting these values back into the original equations confirms that they match.

'Numerical Methods' 카테고리의 다른 글
| 140_Cholesky Decomposition (0) | 2024.04.18 |
|---|---|
| 139_Thomas Algorithm (0) | 2024.04.17 |
| 137_Bairstow's Method Example (0) | 2024.04.15 |
| 136_Bairstow's Method (0) | 2024.04.14 |
| 135_Muller's Method Example (0) | 2024.04.13 |