In this post, I'll explore a simple example using Muller's method, as previously explained in an earlier post. This will provide a practical application of the method to clarify its process and demonstrate how it effectively finds roots of equtaions.
Set the initial values to ${x_0} = 4.5,\,\,\,{x_1} = 5.5,\,\,\,{x_2} = 5$, and use Muller's method to find the roots of the equation.
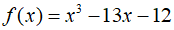
The solution to the above cubic equation is $-3,-1$, and $4$. First, substitute each initial value into the function to calculate their respective values.

Define the various differences as follows.
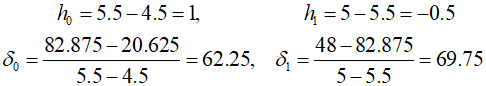
Based on the values above, $a$, $b$, and $c$ can be calculated.
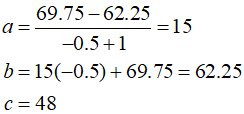
The square root of the discriminant can be calculated as follows.

Therefore, since $\left| {62.25 + 31.54451} \right| > \left| {62.25 - 31.54451} \right|$, the positive sign is used, and the new root estimate can be determined as follows.

The error estimate can be calculated as follows.

Due to the large error, a new estimate assigned. ${x_0}$ is replaced by ${x_1}$, ${x_1}$ by ${x_2}$, and ${x_2}$ by ${x_3}$. Therefore, in the next iteration, the values change as follows.

By repeating the above calculations, this method can rapidly converge to the root.
'Numerical Methods' 카테고리의 다른 글
| 138_Naive Gauss Elimination (0) | 2024.04.16 |
|---|---|
| 137_Bairstow's Method Example (0) | 2024.04.15 |
| 136_Bairstow's Method (0) | 2024.04.14 |
| 134_Muller's Method (0) | 2024.04.12 |
| 133_Newton-Raphson Method (0) | 2024.04.11 |