The Newton method estimates the root on the x-axis through a line between two function values. In contrast, Muller's method adopts a similar approach but projects a parabola through three points. This method involves deriving the coefficients of a parabola that passes through these three points. These coefficients are then used to estimate the point where the parabola intersects the $x$-axis, i.e., the root. This approach can be accessed by formulating the equation of the parabola in a simplified form.
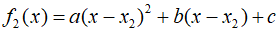
The parabola must intersect at the three specified points, and the coefficients of the above equation can be calculated by substituting the values of each of these three points.

Considering that the third term is zero, $f({x_2})=c$. Therefore, by substituting this result into the above two equations, we can obtain two equations with two unknowns.
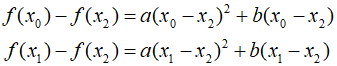
To find the remaining coefficients $a$ and $b$, algebric manipulation can be utilized. This involves using methods to define various differences.
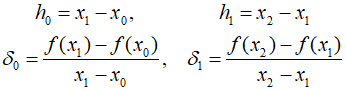
Upon substituting and rearranging the equations, the formulation can be summarized as follows.

Solving for $a$ and $b$, the results can be expressed as follows.
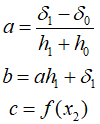
Finding the roots of the above equations, the results are as follows.

Use of quadratic equations allows for the determination of both real and complex solutions. Additioanlly, the above formulation can be used to estimate the approximate error.

In the problem described, the denominator's two roots provide two possible solutions. In Muller's method, the root corresponding th the sign of $b$ that matches is chosed. This choice results in the largest denominator, uielding the root estimate closest to ${x_2}$. Once ${x_3}$ is determined, a decision is made during the iteration process about which point should be discarded.
Typically, when searching only for real roots, the two nearest original points to the new root estimate ${x_3}$ are selected. If both real and complex roots are being calculated, each time a new ${x_3}$ value is determined, the previous values sequentially replace their roles. This systematic approach facilitates the convergence towards the most accurate root estimation while adapting to the dynamic nature of the solutions.
'Numerical Methods' 카테고리의 다른 글
| 138_Naive Gauss Elimination (0) | 2024.04.16 |
|---|---|
| 137_Bairstow's Method Example (0) | 2024.04.15 |
| 136_Bairstow's Method (0) | 2024.04.14 |
| 135_Muller's Method Example (0) | 2024.04.13 |
| 133_Newton-Raphson Method (0) | 2024.04.11 |