Newton-Raphson method is one of the methods used to numerically find the roots of a nonlinear equation. It is characterized by its rapid convergence of approximations to the actual solution, although its convergence speed and whether it converges at all can depend on the starting point.
In this post, I'll geometrically derive the Newton-Raphson formula using Taylor series expansion.
Firstly, the Taylor series expansion of a function $f(x)$ is as follows.

Here, $\xi $ is located somewhere between ${x_i}$ and ${x_{i + 1}}$, and considering only up to the first derivative term, it can be approximated as follows.
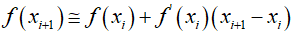
Assuming that the function intersects the $x$-axis at ${x_{i + 1}}$, where $f\left( {{x_{i + 1}}} \right) = 0$, using the above approximation results in the following equation.
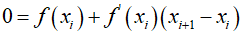
When the equation is rearranged to solve for ${x_{i + 1}}$, it yields the Newton-Raphson formula.
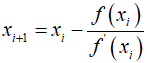
In addition to suvh induction processes, Taylor series can also be utilized to estimate the error of a formula. Here, a complete Taylor series is used to obtain precise results. When ${x_{i + 1}} = {x_r}$ and $\sqrt x $ is the actual value, the initially expanded Taylor series is represented as follows.
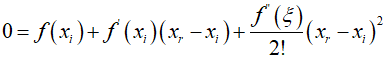
In the above expression, by subtracting the previously derived approximation, only the error term can be isolated.
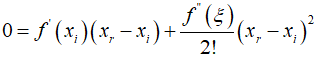
Here, using the error ${E_{t,i + 1}} = {x_r} - {x_{i + 1}}$, it can be expressed as follows.
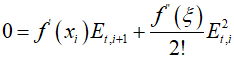
Both ${x_i}$ and $\xi $ will ultimately be approximated by the square root value, and are rearranged as follows.

Therefore, through the above expression, it can be understood that the error is proportional to the square of the previous error. This represents quadratic convergence, where the number of accurate decimal places approximately doubles with each iteration.Consequently, this indicates that the Newton-Raphson method can converge very rapidly.
'Numerical Methods' 카테고리의 다른 글
| 138_Naive Gauss Elimination (0) | 2024.04.16 |
|---|---|
| 137_Bairstow's Method Example (0) | 2024.04.15 |
| 136_Bairstow's Method (0) | 2024.04.14 |
| 135_Muller's Method Example (0) | 2024.04.13 |
| 134_Muller's Method (0) | 2024.04.12 |