The content on machine learning is based on studies from various books and papers, primarly focusing on Chris Bishop's "Deep Learning - Foundations and Concepts"
In machine learning, it is essential to deal with uncertainty. For example, this is because a system that classifies dogs and cats cannot actually achieve perfect accuracy.
Uncertainty can be broadly divided into two types. The first is known as epistemic uncertainty or systematic uncertainty, which occures due to the finite size of data. Even if the dataset is expanded to an infinitely largy size, perfect accuracy cannot be achieved due to the second type of uncertainty.
The second type of uncertainty is known as aleatoric uncertainty or simply as noise. Typically, this kind of noise arises because we can only observe partial information. Therefore, to reduce such uncertainty, it is essential to collect various types of data.
Both types of uncertainty are handled using the framework of probability theory, and these rules, combined with decision theory, allow us to make optimal predictions by considering all possible information, even if the information is incomplete or ambiguous in principle.
The probability that $X$ takes the value ${x_i}$ can be denoted as $p(X={x_i})$. Additionally, to represent the distribution for the random variable $X$, or to represent the distribution for a specific value ${x_i}$, we use $p({x_i})$.
The two fundamental rules of probability theory can be stated as follows.
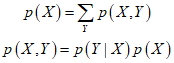
Here, ${p\left( {X,Y} \right)}$ represents the joint probability, meaning "the probability of $X$ and $Y$". Similarly, $p\left( {Y|X} \right)$ represents the conditional probability, meaning "The probability of $Y$ given $X$". Lastly, $p\left( X \right)$ denotes the probability of $X$.
Using the multiplication rule and the symmetry property, the following relationship between conditional probabilities can be derived.
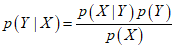
This equation is known as Bayes' theorem, and it plays an important role in machine learning. This is because it allows us to relate the conditional distribution on the left side to the reverse direction conditional distribution on the right side.

Using the sum rule, the denominator can be expressed in terms of the quantities apperaing in the numerator. This allows us to calculate the marginal probability along with the conditional probability for a given case.
In addition to probabilities defined for discrete sets, let's consider probabilities for contunous variable with infinite precision is very low, the probability concept used so far cannot be applied. Therefore, we must use the concept of a probability density function.
Thre probability that $x$ belongs to the interval $\left( {x,x + \delta x} \right)$ is $p\left( x \right)\delta x$, where $\delta x$ is a small value close to 0. The probability that $x$ exists in the interval $(a,b)$ is as follows.

Since probabilities cannot be negative, the following two conditions must be satisfied.
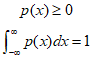
The sum and product rules for probability densityes, as well as Bayes' theorem, also apply to probability distributions for combinations of continuous and discrete variables. When $x$ and $y$ are two real variables, the sum and product rules can be represented as follows.

Similarly, Bayes' theorem can be expressed as follows.

ref : Chris Bishop's "Deep Learning - Foundations and Concepts"
'Deep Learning' 카테고리의 다른 글
| 55_Likelihood Function (0) | 2024.01.24 |
|---|---|
| 54_Linear Regression (0) | 2024.01.23 |
| 53_Bernoulli, Binomial, and Multinomial Distribution (0) | 2024.01.22 |
| 52_Gaussian Distribution (0) | 2024.01.21 |
| 51_Distribution (0) | 2024.01.20 |