A symmetric matrix is defined by the property ${a_{ij}} = {a_{ji}}$ for all $i$ and $j$, meaning $A={A^T}$. Such systems are common in mathematical and engineering problems and offer computational advantages because they require only half the storage space and, in most cases, only half the computation time needed for solving.
Today, I'll explain the Cholesky decomposition, which is based on the fact that a positive definite matrix can be represented as the product of a lower triangular matrix and its transpose. This method is especially useful for efficiently solving linear systems and computing matrix inverses in numerical simulations.
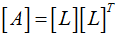
Therefore, compared to other algorithms, Cholesky decomposition has the advantage of being numeriacally stable and takes only about half the time of LU decompostion, resulting in fewer errors. The equations can be expanded and set to be equivalent. The results can be expressed in a simple recursive relationship as follows.

Through an example to explain this algorithm.

For the first row, use the above formula to perform the calculation.
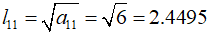
And the second row,
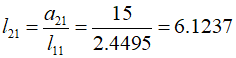
Then, using the second equation, it can be calculated as follows.

And the third row,
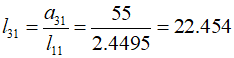
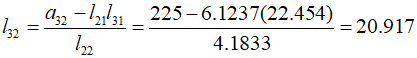
Therefore,
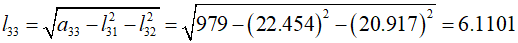
Therefore, the Cholesky decomposition can be represented as follows.
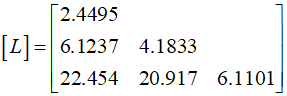
To verify the result, use MATLAB to check if the product of the transpose of the lower triangular matrix recreates the original matrix.
L = [2.4495 0 0;
6.1237 4.1833 0;
22.454 20.917 6.1101];
A = round(L*transpose(L))

This confirms that the Cholesky decomposition was performed correctly.
'Numerical Methods' 카테고리의 다른 글
| 142_Golden-Section Search (0) | 2024.04.20 |
|---|---|
| 141_Gauss-Seidel Method (1) | 2024.04.19 |
| 139_Thomas Algorithm (0) | 2024.04.17 |
| 138_Naive Gauss Elimination (0) | 2024.04.16 |
| 137_Bairstow's Method Example (0) | 2024.04.15 |