In the last post(76_Topology Optimization using Optistruct), I attempted a compliance minimization topology optimization problem in Optistruct. I wanted to compare it with Sigmund's paper, so I tried a simple setup, but it was difficult to make an accurate comparision, and more importantly, the results were not sarisfactory to me.
The biggest advantage of using commercial software for optimization is that there's no need to write the extensive code required for finite element analysis. Additionally, the interface allows for intuitive and convenient settings adjustments necessary for analysis.
For example, if you were to write finite element analysis code directly through coding, you would need to specifiy coordinate indexes or directly set position coordinate values. This could lead to potential errors, and you would only know if the boundary conditions were correctly input after running the code.
However, using commercial software allows you to visually inspect and select options directly, reducing the risk of errors and enabling you to know if the boundary conditions have been properly applied without having to run the analysis.
But, using commercial software restricts you to only the methods set up in the softwere, limiting your options and making it impossible to try new approaches. Therefore, from my perspective as someone studying algorithms, commercial software has been used merely as a verify the correctness of my code's results.
So today, solve various optimization problems using Optistruct. I will not delve into the detailed settings or processes of the program but will focus on explaining only the key aspects.
First, solve a commonly used examples.


For a cantilever beam with one end fixed and a load applied to the lower part of the opposite end, the shape displayed in Optistruct was an described. The volume constraint is 0.5, and the tolerance is 0.05. The plot shows only iso values above 0.5.
Additionally, topology optimization can be performed similarly for the multiple load case that was presented as an example in the 99line code.
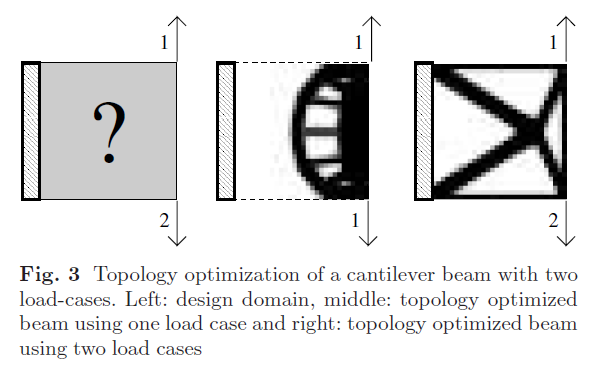

Without an Iso plot, the result appears as shown. In the picture, the left side shows an unstable appearance as if floating because two forces of the same magnitude were applied in the same load step, which does not satisfy the fixed conditions and indicates an incorrect setup. To correctly apply multiple loads as shown in the right photo, each force must have its own load step set.
The examples above were topology optimization problem that minimize compliance under volume constraint conditions, but other types of problems can also be solved. If you conduct topology optimization with displacement constraints and volume as the objective function, you can obtain results like the following.
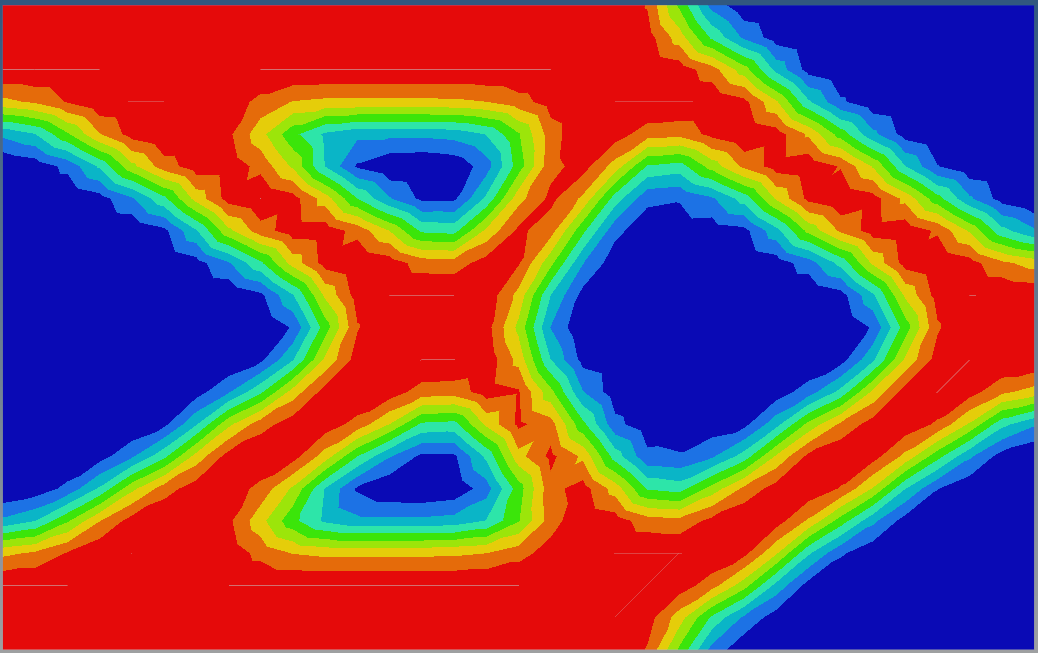
In the cantilever beam example, the load was moved from the bottom right to the middle right. Additionally, problems involving the maximization of natural frequency can also be easily solved through Optistruct.
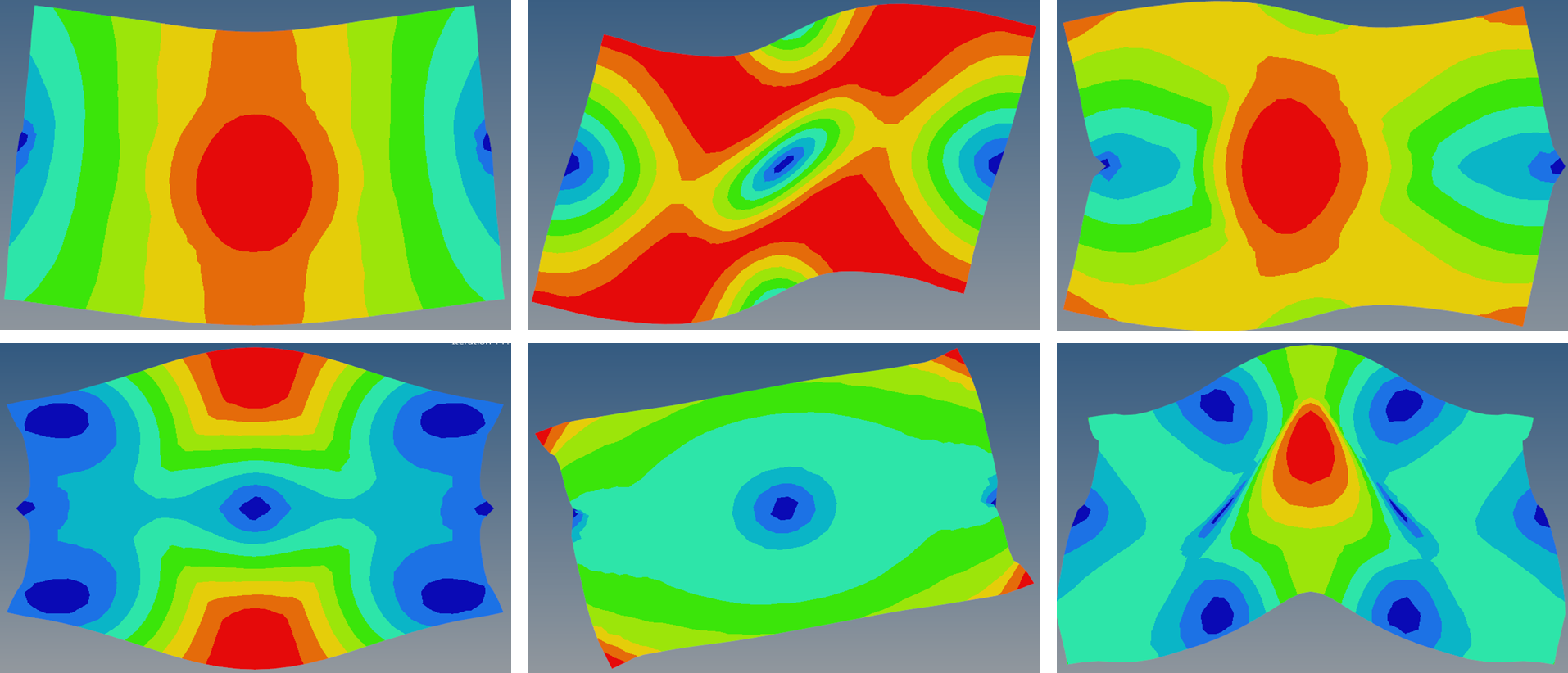
The results are for the maximizatio of natural frequencies, showing the mode shapes from the first to the sixth modes, starting from the top left.
Although it is possible to solve many more and diverse problems than the examples above, today we only proceeded with simple two-dimensional examples.
'Structural Analysis > OptiStruct' 카테고리의 다른 글
| 76_Topology Optimization using Optistruct (0) | 2024.02.14 |
|---|---|
| 22_Mid rail analysis (1) | 2023.12.22 |
| 21_Fluid Structure Coupling(2) (1) | 2023.12.21 |
| 20_Fluid Structure Coupling (0) | 2023.12.20 |
| 14_Pendulums(2) (0) | 2023.12.14 |