In a previous post, we saw that the forward encoder model is defined as a sequence of Gaussian conditional distributions, and today, we'll write about additional content. Inverting the encoder model becomes a challenging distribution to handle because it requires intergrating over all possible starting vector values ${\text{x}}$ for the unknown data distribution $p({\text{x}})$ we aim to model.
Therefore, an approximation of the distribution is learned using the distribution $p({{\text{z}}_{t - 1}}|{{\text{z}}_t},{\text{w}})$, controlled by a neural network representing the weights and biases ${\text{w}}$. Through the trained network, simple Gaussian distribution samples ${{\text{z}}_T}$ can be sampled and transformed into samples of the data distribution $p({\text{x}})$ by iteratively applying the network through the process of reverse sampling steps.
By performing a Taylor series expension around ${{\text{z}}_t}$ for ${{\text{z}}_{t-1}}$ as a function, it can be seen that $q({{\text{z}}_{t - 1}}|{{\text{z}}_t})$ can be approximated as Gaussian. This shows that the reverse distribution $q({{\text{z}}_t}|{{\text{z}}_{t - 1}})$ from a small distribution has values close to the coveriance of the forward noise process $q({{\text{z}}_{t - 1}}|{{\text{z}}_t})$. Therefore, the reverse process can be modeled in the form of a Gaussian distribution as follows.
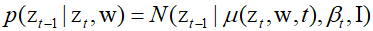
Here, $\mu ({{\text{z}}_t},{\text{w}},t)$ is a deep neural network regulated by a series of parameters ${\text{w}}$. The network uses the index $t$ as an input to account for changes in variance $t$ at different stages of the chain. This allows the use of a single network to inverse the entire Markov chain, instead of training separate networks for each step.
Since the output and input must have the same dimensions, there is considerable flexibility in choosing the architecture of the neural network used to model $\mu ({{\text{z}}_t},{\text{w}},t)$. Given these constraints, the U-net architecture is commonly used in image processing applications. The entire denoising process takes the form of the following Markov chain.
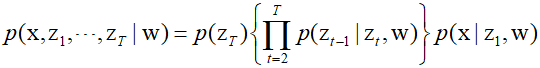
Assuming that $p({{\text{z}}_T})$ is the same as the distribution $q({{\text{z}}_T})$, it is $N({{\text{z}}_T}|0,{\text{I}})$. First, sample a simple Gaussian distribution, sequentially sample from each conditional distribution $p({{\text{z}}_{t - 1}}|{{\text{z}}_t},{\text{w}})$, and finally, sample from $p({\text{x}}|{{\text{z}}_1},{\text{w}})$ to obtain a sample ${\text{x}}$ in the data space.
To train the neural network, an objective function must be determined. Here, the likelihood function for the data point ${\text{x}}$ is set as the objective function, represented as follows.

The above euqation is an example of a general latent variable model where the latent variables are composed of ${\text{z}}$ and the observed variables are ${\text{x}}$. The latent variables all have the same dimensions as the data space, which is different from the case with Generative Adversarial Networks.
When the exact likelihood is difficult to resolve, a method similar to that used by Variational Autoencoders can be adopted to maximize the lower bound of the log likelihood. This is called the Evidence Lower Bound(ELBO), and when any arbitrary $q({\text{z}})$ distribution is chosen, the following relationship holds.
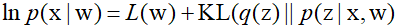
Here, $L$ represents the evidence lower bound, also known as the variational lower bound. Furthermore, the Kullback-Leibler divergence between two probability density functions $f({\text{z}})$ and $g({\text{z}})$ is denoted as ${\text{KL}}(f||g)$, and the respectives equations are as follows.
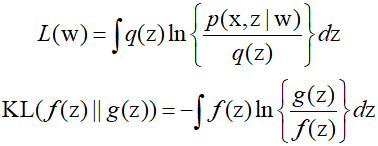
Therefore, summarizing the above equations, since the Kullback-Leibler divergence is greater than 0, the following holds true.
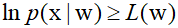
Optimizing the optimal distribution $q({\text{z}})$ makes the lower bound tighter, making the parameter optimization of $p({\text{x}},{\text{z}}|{\text{w}})$ more similar to maximizing the likelihood. However, in the case of diffusion models, the adjustable parameters are only for the model $p({\text{x}},{{\text{z}}_1}, \cdots ,{{\text{z}}_T}|{\text{w}})$ of the reverse Markov chain. By leveragin the flexibility in choosing $q({\text{z}})$ to vary according to ${\text{x}}$, and upon organizing the equation, the ELBO can be written in the following form.
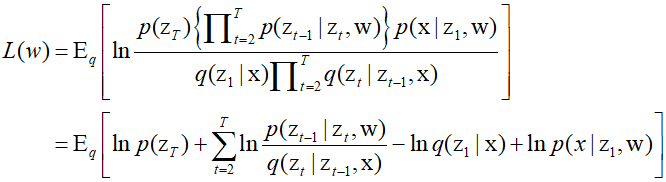
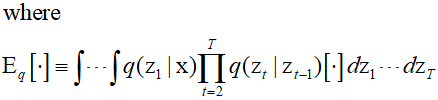
The first term on the right side of the above equation can be excluded since it contains no trainable parameters.
'Deep Learning' 카테고리의 다른 글
| 98_Simple ANN Example Using PyTorch(2) (0) | 2024.03.07 |
|---|---|
| 97_Simple ANN Example Using PyTorch (0) | 2024.03.06 |
| 73_Diffusion Model (0) | 2024.02.11 |
| 72_Generative Adversarial Networks (1) | 2024.02.10 |
| 71_Graph Convolutional Network (0) | 2024.02.09 |