In optimization, instead of directly computing the inverse of the Hessian in each iteration, the Hessian itself can be updated. There are various methods to achieve this, but in this post, I'll explain one of the most commonly used methods the Broyden-Fletcher-Goldfarb-Shanno(BFGS) method.
First, estimate the initial design ${x^{(0)}}$ and choose a symmetric positive definite matrix ${{\text{H}}^{(0)}}$ as the estimate of the Hessian of the cost function. ${{\text{H}}^{(0)}}$ can also be the identity matrix. Next, select the convergence parameter $\varepsilon $, set $k=0$, and calculate the gradient vector ${{\text{c}}^{(0)}} = \nabla f({x^{(0)}})$.
Calculate the norm of the gradient vector $\left\| {{{\text{c}}^{(k)}}} \right\|$. If $\left\| {{{\text{c}}^{(k)}}} \right\| < \varepsilon $, terminate the optimization process otherwise, continue.
Solve the equation of the linear system to obtain the search direction.

Calculate the optimum step size, and use the calculated value along with the search direction to update $x$.

Afterwards, update the approximation of the Hessian of the cost function.

Where ${{\text{D}}^{(k)}}$ and ${{\text{E}}^{(k)}}$ are correction matrices, which can be calculated as follows.
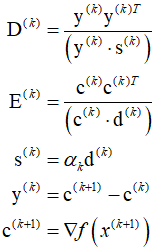
Set $k=k+1$ and repeat the above process untill the convergence criteria are satisfied.
The first iteration of the BFGS mothod, then ${\text{H}}$ is ${\text{I}}$, is identical to the steepest descent mothod. The BFGS update formula shows that, with exact line search, the approximation of the Hessian is kept positive definite, ensuring that the search direction is a descent direction for the cost function.
However, numerically, due to incomplete line search, rounding errors, etx., the Hessian may become singular or indefinite, so measures to prevent this should be included in the algorithm process. Using a numerical procedure to update the Cholesky factors of the Hessian is very useful, as it helps maintain the matrix numerically positive definite and solves linear equations more efficiently.
'Optimization Technique' 카테고리의 다른 글
| 124_Linearization (0) | 2024.04.02 |
|---|---|
| 123_BFGS Method Example (0) | 2024.04.01 |
| 121_DFP Method Example (0) | 2024.03.30 |
| 120_Inverse Hessian Updating (0) | 2024.03.29 |
| 119_Modified Newton Method (0) | 2024.03.28 |