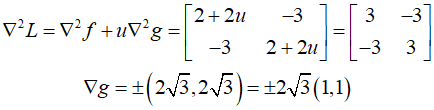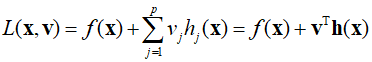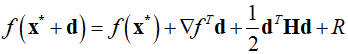Finite

In this post, I'll study the second-order necessary and sufficient conditions for optimization probles with constraints. Similar to the unconstrained case, the second part of the Taylor expansion of function at ${x^*}$ is used to determine whether that point is a local minimum. In the presence of constraints, the active constriants at ${x^*}$ must also be considered to determine a feasible chang..

In optimization problems, getting a satisfying answer to "How can the optimal solution be found?" is not straightforward. However, if the optimization problem can be proven to be convex, any local minimum also becomes a global minimum. Furthermore, the KKT necessary conditions are not only necessary but also sufficient for minimum point. In this post, I will study convex functions and their prop..

In this post, I intend to explain the "Karush-Kuhn-Tucker (KKT) Optimality Conditions," widely used in optimization theory. The KKT conditions can be applied to optimization problems with both equality and inequality constraints. They can be considered a more generalized form of the Lagrangian function described in the previous post(105_Lagrange Multiplier Theorem). In this problem, there are bo..

The Lagrange Multiplier Theorem is a technique used to solve the provlem of finding the extrema of multivariable functions under specific constraints. This method is very effective for solving optimization problems with constrains. In this post, I will explain using an example of an optimization problem with equality constraints. Assuming that $x$ is a regular point where it is a local minimum, ..

The concept of Taylor's expansion is essential in optimal design and numerical methods. Taylor's expansion is a mathematical formula that approximates the value of a function near a specific point using the derivatives of the function at that point. In other words, it can be considered a generalization of linear approximation in the form of a polynomial function. It is very useful when attemptin..