Today, I plan to briefly explain how to apply the dual method through an example, as dexcribed in the previous post(110_More on Duality).
The definition of the problem is as follows. Let's find the dual ans solve it.

To solve the above primal problem using optimality conditions, First need to fine the Lagrangian. The Lagrangian for the given problem is as follows.
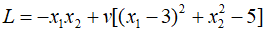
Where $v$ is the Lagrange multiplier, used to integrate the constraints into the objective function. To find the solution to the optimization proble, we use the first-order necessary conditions of the Lagrangian. This means differentiating the Lagrangian with respect to each variable and setting it to zero, resulting in the following equations.

The solutions to the above equations can be calculated through MATLAB as follows.
syms x1 x2 v
eqns = [((x1-3)^2)+x2^2==5, -x2+(2*x1-6)*v==0, -x1+2*x2*v==0];
vars = [x1 x2 v];
[solx1, solx2, solv]=solve(eqns, vars)
The Hessian function, which is the second derivative of the Lagrangian, is as follows.
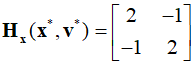
The Hessian matrix is used to determine the nature of the solution in optimization problems. Since this Hessian matrix is positive definite, it indicates that the solution is a local minimum. Therefore, near the solution of the original problem, we can define and analyze the dual problem.

Using the given constratins, ${x_1}$ and ${x_2}$ can be expressed as functions of $v$ when $4{v^2} - 1 \ne 0$.

Substituting the above expression into the Lagrangian, the dual function can be derived as follows.

This is valid when $v \ne \pm \frac{1}{2}$, and the dual function has a local maximum at ${v^*}=1$. Furthermore, substituting $v=1$ into the above expressions for ${x_1}$ and ${x_2}$ yields the same result as the solution to the original problem.
'Optimization Technique' 카테고리의 다른 글
| 115_KKT Conditions for LP Problem (0) | 2024.03.24 |
|---|---|
| 114_Linear Programming (0) | 2024.03.23 |
| 110_More on Duality (0) | 2024.03.19 |
| 109_Duality (0) | 2024.03.18 |
| 108_Second-order Conditions (0) | 2024.03.17 |