In a previous post(109_Duality), we touched on duality, but there were many areas where the explanation was lacking, and establishing a duality relationship requires additional formulations. Therefore, in this post, I intend to explain the necessary additional formulations.
${\bf{x}}({\bf{v}})$ denote the local minimum of the Lagrangian function, as follows.
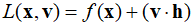
The dual function can be written as follows.
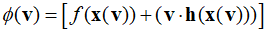
Here, ${\bf{x}}({\bf{v}})$ is the solution to the necessary conditions. Differentiating the above expression with respect to ${\bf{v}}$ and considering that ${\bf{x}}({\bf{v}})$ is a differentiable function of ${\bf{v}}$, it can be represented as follows.
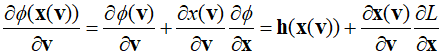
Since $\frac{{\partial {\bf{x}}({\bf{v}})}}{{\partial {\bf{v}}}} = 0$ because ${{\bf{x}}({\bf{v}})}$ minimizes the above Lagrangian function, the following equation consequently hold true.
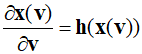
From the description of the above equation, its clear that calculating the gradient of the dual function is quite straightforward. After minimizing the dual function with respect to ${\bf{x}}$, it's possible to calculate the gradient of ${\bf{h}}({\bf{x}})$, which corresponds to $\phi ({\bf{v}})$.
Differentiating the above equation with respect to ${\bf{v}}$ yields the following Hessian.

To calculate $\frac{{\partial {\bf{x}}({\bf{v}})}}{{\partial {\bf{v}}}}$, differentiate the necessary conditions with respect to ${\bf{v}}$ to derive the following equation.
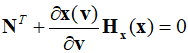
Upon rearranging the terms for $\frac{{\partial {\bf{x}}({\bf{v}})}}{{\partial {\bf{v}}}}$, the equation can be expressed as follows.
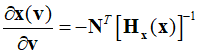
Therefore, by simplifying the equation, the following Hessian can be obtained.
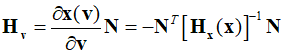
Since ${\left[ {{{\bf{H}}_{\bf{x}}}({\bf{x}})} \right]^{ - 1}}$ is positive definite and ${\bf{N}}$ is full column rank in the near of ${\bf{x}}$, ${{{\bf{H}}_{\bf{x}}}({\bf{x}})}$ becomes a negative definite $n \times n$ matrix.
'Optimization Technique' 카테고리의 다른 글
| 114_Linear Programming (0) | 2024.03.23 |
|---|---|
| 113_Dual Problem (0) | 2024.03.22 |
| 109_Duality (0) | 2024.03.18 |
| 108_Second-order Conditions (0) | 2024.03.17 |
| 107_Convex Functions (0) | 2024.03.16 |